0898-08980898 13876453617
在上篇文章中,我们介绍了程序优化器框架 egg,以及它如何利用 Equality Saturation 方法来对表达式进行优化。关于 Equality Saturation 最近我还看到 @太极图形 发布了一个 talk 来介绍这一技术,算是中文互联网上为数不多的技术资料,推荐感兴趣的朋友们观看。
这篇文章我们将介绍如何用 egg 实现一个真正的 SQL 优化器。其中会涉及以下经典的优化技术:
使用这些技术,我们的优化器就可以对日常简单查询(例如 TPC-H 中不含子查询的 Q1/3/5/6/10)给出不错的结果,并且在 egg 中实现它们也只需要几百行代码。
我认为这是一个非常适合上手实践,以深入理解优化器基本原理的好机会。为此我们尝试设计了 sql-optimizer-labs 实验,大家可以理解为是这篇文章的配套练习。感兴趣的读者可以在读完本文后尝试实现自己的 SQL 优化器,并挑战其中设置的一系列测例。如果想阅读完整代码,或了解它在实际数据库中的应用,可以直接参考 RisingLight 的计划器模块。
我们首先回顾一下上篇文章中在 egg 里定义的 SQL 语言。在后面的内容中可能会频繁引用到。
define_language! {
pub enum Expr {
// values
Constant(DataValue), // null, true, 1, 1.0, "hello", ...
Column(ColumnRefId), // $1.2, $2.1, ...
// operations
"+" = Add([Id; 2]), // (+ a b)
"and" = And([Id; 2]), // (and a b)
// list
"list" = List(Box<[Id]>) // (list ...)
// plans
"scan" = Scan([Id; 2]), // (scan table[column..])
"proj" = Proj([Id; 2]), // (proj[expr..]child)
"filter" = Filter([Id; 2]), // (filter condition child)
"join" = Join([Id; 4]), // (join type condition left right)
"inner" = Inner,
"left_outer" = LeftOuter,
"right_outer" = RightOuter,
"full_outer" = FullOuter,
"agg" = Agg([Id; 3]), // (agg aggs=[expr..]group_keys=[expr..]child)
// expressions must be agg
// output=aggs || group_keys
"order" = Order([Id; 2]), // (order[order_key..]child)
"asc" = Asc(Id), // (asc key)
"desc" = Desc(Id), // (desc key)
"limit" = Limit([Id; 3]), // (limit limit offset child)
}
}
对于这样一条 SQL 语句:
SELECT users.name, count(commits.id)
FROM users, repos, commits
WHERE users.id = commits.user_id
AND repos.id = commits.repo_id
AND repos.name = 'RisingLight'
AND commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
GROUP BY users.name
HAVING count(commits.id) >= 10
ORDER BY count(commits.id) DESC
LIMIT 10它的执行计划可以用我们定义的语言表示成这样的形式:
(proj (list $1.2 (count $3.1))
(limit 10 0
(order (list (desc (count $3.1)))
(filter (>= (count $3.1) 10)
(agg (list (count $3.1)) (list $1.2)
(filter (and (and (and (= $1.1 $3.2) (= $2.1 $3.3)) (= $2.2 'RisingLight'))
(and (>= $3.4 '2022-01-01') (<= $3.4 '2022-12-31')))
(join inner true
(join inner true
(scan $1 (list $1.1 $1.2 $1.3))
(scan $2 (list $2.1 $2.2 $2.3)))
(scan $3 (list $3.1 $3.2 $3.3 $3.4 $3.5))
)))))))我们现在要做的就是定义一系列规则对上述表达式进行等价变换,最终找到一个代价最小的表示作为优化结果。
首先最简单的优化当属合并或消除无效算子。
例如条件恒为 true 的 Filter 算子可以直接消除:
rewrite!("filter-true"; "(filter true ?child)" => "?child")
而条件恒为 false 的 Filter 算子则不生成任何数据。我们引入一种 Empty 节点来表示一个空表:
rewrite!("filter-false"; "(filter false ?child)" => "(empty ?child)")
注意到我们将原来的子节点包在了 empty 中,这样可以在优化后保留算子的 schema 信息,也就是每一列的名称和类型。
类似地,我们还可以对其它算子进行化简:
rewrite!("limit-null"; "(limit null 0 ?child)" => "?child"),
rewrite!("limit-0"; "(limit 0 ?offset ?child)" => "(empty ?child)"),
rewrite!("order-null"; "(order (list) ?child)" => "?child"),
rewrite!("inner-join-false"; "(join inner false ?l ?r)" => "(empty (join inner false ?l ?r))"),
// 注意:对于其它 outer join,条件为 false 并不能推出结果为空
接下来,底层算子生成的 Empty 节点可以进一步向上传播。如果一直传到了最顶层,那就说明整个查询的结果是一个空表。
rewrite!("proj-on-empty"; "(proj ?exprs (empty ?c))" => "(empty ?exprs)"),
rewrite!("filter-on-empty"; "(filter ?cond (empty ?c))" => "(empty ?c)"),
rewrite!("order-on-empty"; "(order ?keys (empty ?c))" => "(empty ?c)"),
rewrite!("limit-on-empty"; "(limit ?limit ?offset (empty ?c))" => "(empty ?c)"),
rewrite!("inner-join-left-empty"; "(join inner ?on (empty ?l) ?r)" => "(empty (join inner false ?l ?r))"),
rewrite!("inner-join-right-empty"; "(join inner ?on ?l (empty ?r))" => "(empty (join inner false ?l ?r))"),
// 同样对于 outer join 不一定成立
// 另外可以考虑一下:agg-on-empty 的结果是什么
另一方面,两个相邻的算子有机会进行合并。
比如两个相邻 Filter 算子可以合并为一个 Filter:
rewrite!("filter-merge";
"(filter ?cond1 (filter ?cond2 ?child))" =>
"(filter (and ?cond1 ?cond2) ?child)"
)
相邻的 Limit 和 Order 算子则可以合并为一个 TopN 算子:
rewrite!("limit-order-topn";
"(limit ?limit ?offset (order ?keys ?child))" =>
"(topn ?limit ?offset ?keys ?child)"
)
由于 TopN 算子使用二叉堆来维护前 K 大的元素,复杂度为 O(NlogK),而 Order 算子进行全员排序的复杂度为 O(NlogN),因此 TopN 通常会比 Limit + Order 具有更低的开销。
接下来稍微 non-trivial 一点的经典优化是谓词下推(Predicate Pushdown)。
在上面的 SQL 语句中,我们看到 WHERE 子句存在大量谓词条件,对应到执行计划中就是 Join 算子上面的 Filter 算子:
Filter: users.id = commits.user_id
│ AND repos.id = commits.repo_id
│ AND repos.name = 'RisingLight'
│ AND commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
└─Join: inner, on=true
├─Join: inner, on=true
│ ├─Scan: users [id, name, email]
│ └─Scan: repos [id, name, url]
└─Scan: commits [id, user_id, repo_id, time, message]而实际上,其中有些谓词条件都只和一个表相关,另一部分则是 Join 的连接条件。因此我们可以将这些谓词下推到底层算子上,来更早地过滤掉不需要的数据,从而降低上层算子要处理的数据量。下推之后的执行计划如下所示:
Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Join: inner, on=true
│ ├─Scan: users [id, name, email]
│ └─Filter: repos.name = 'RisingLight'
│ └─Scan: repos [id, name, url]
└─Filter: commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
└─Scan: commits [id, user_id, repo_id, time, message]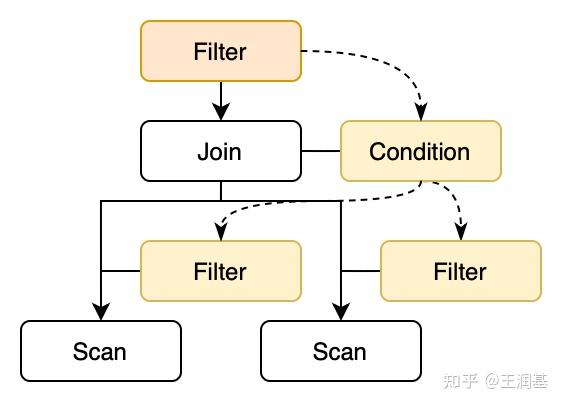
观察 Filter 算子的下推路径,我们发现可以分解为两个步骤:
第一步看起来非常简单,因为无需任何附加条件:
rewrite!("pushdown-filter-join";
"(filter ?cond (join inner ?on ?left ?right))" =>
"(join inner (and ?on ?cond) ?left ?right)"
)
但是第二步就比较棘手了,因为这里有三种可能情况:
此时我们就需要搬出 egg 的条件重写功能了。只有当谓词中引用的列满足一定条件时,我们才能把它推下去:
rewrite!("pushdown-filter-join-left";
"(join inner (and ?cond1 ?cond2) ?left ?right)" =>
"(join inner ?cond2 (filter ?cond1 ?left) ?right)"
if columns_is_subset("?cond1", "?left")
),
rewrite!("pushdown-filter-join-right";
"(join inner (and ?cond1 ?cond2) ?left ?right)" =>
"(join inner ?cond2 ?left (filter ?cond1 ?right))"
if columns_is_subset("?cond1", "?right")
),
// 注:需配合 AND 交换率和结合律规则共同使用,才能保证所有谓词都被下推
这里函数 columns_is_subset(a, b) 的语义为:表达式 a 所使用的列的集合,是否包含于算子 b 所提供的列的集合。为此我们需要引入新的表达式分析:Column Analysis。
如果读者曾经学过程序分析或编译优化的相关课程,相信能够看出,这其实就类似于经典的 活跃变量分析。上面的两个集合分别对应于活跃变量分析中的 use 和 def集。而由于我们只需要对表达式节点计算 use,对 SQL 算子计算 def,因此实际操作中可以将二者合并为同一个变量来表示。
具体分析的核心代码如下所示:(完整代码可参考 RisingLight)
/// Column Analysis 的分析结果类型:一个 column 集合
pub type ColumnSet = HashSet<ColumnRefId>;
/// 对于表达式节点,返回使用的列
/// 对于 SQL 算子节点,返回定义的列
pub fn analyze_columns(egraph: &EGraph, enode: &Expr) -> ColumnSet {
use Expr::*;
let x = |i: &Id| &egraph[*i].data.columns;
match enode {
// 对于 Column 节点,返回包含自己的集合
Column(col) => [*col].into_iter().collect(),
// 对于 Proj 和 Agg,返回所有表达式的并集
Proj([exprs, _]) => x(exprs).clone(),
Agg([exprs, group_keys, _]) => x(exprs).union(x(group_keys)).cloned().collect(),
// 对于其它类型,返回所有子节点的并集
_ => (enode.children().iter())
.flat_map(|id| x(id).iter().cloned())
.collect()
}
}
这段代码虽然短,但是很有效。这里我们通过一些例子来说明这段分析的效果:
// 表达式 => Column 集合
// use
'RisingLight' => {}
$2.2 => { $2.2 }
(= $2.2 'RisingLight') => { $2.2 } = A
(= $1.1 $3.2) => { $1.1 $3.2 } = B
// def
(scan $2 (list $2.1 $2.2 $2.3)) => { $2.1 $2.2 $2.3 } = C
(join inner true
(scan $1 (list $1.1 $1.2 $1.3))
(scan $2 (list $2.1 $2.2 $2.3))) => { $1.1 $1.2 $1.3 $2.1 $2.2 $2.3 } = D
(scan $3 (list $3.1 $3.2 $3.3 $3.4 $3.5)) => { $3.1 $3.2 $3.3 $3.4 $3.5 } = E
(proj (list $1.2 (count $3.1)) ..) => { $1.2 $3.1 }由于 A ? C ? D,因此(=$2.2 'RisingLight') 这个谓词面对 (join (join $1 $2) $3)时会先推到左子树,再推到右子树;而另一方面 B ? D, B ? E,所以 (=$1.1 $3.2) 无法下推,最终只能留在 Join 的条件上。
和谓词下推类似,我们还可以将 Projection 算子下推,来更早地丢掉不再使用的列。这一优化称为投影下推(Projection Pushdown)。更进一步,当 Projection 算子被一路下推到最底层的 Scan 算子上时,我们就可以直接去掉 Scan 算子中没有被使用的列,从而减少读入数据的开销。这一过程称为列裁剪(Column Pruning)。
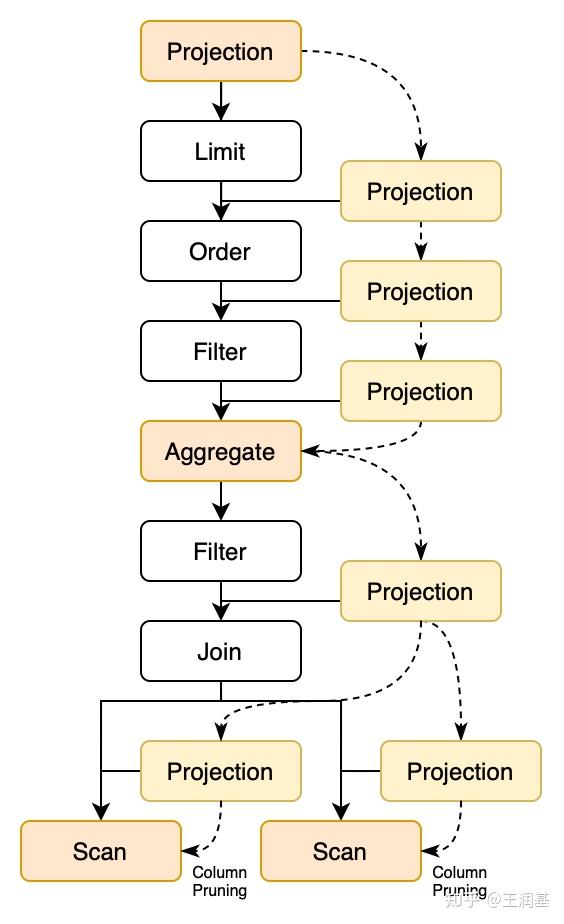
对于一条 SELECT 查询语句,它最原始的执行计划中 Projection 算子通常在最顶层。如果包含聚合操作,那么在执行计划树的中间还会存在一个 Aggregate 算子,它也可以看作一种特殊的 Projection。这两种算子是投影下推的起点。在下推过程中,Projection 会不断吸收中途算子使用的列,直到遇到 Projection、Aggregate 或 Scan 三种算子中的一个。这三种算子都是根据自己的表达式而不是由子节点来决定输出的列,因此可以对它们进行列剪裁。
在上一节中,我们已经将查询中的 Filter 算子下推到了 Join 子树里:
Aggregate: count(commits.id), groupby=users.name
└─Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Join: inner, on=true
│ ├─Scan: users [id, name, email]
│ └─Filter: repos.name = 'RisingLight'
│ └─Scan: repos [id, name, url]
└─Filter: commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
└─Scan: commits [id, user_id, repo_id, time, message]接下来,我们继续从 Aggregate 开始做投影下推。这一过程在每层算子之间都插入了新的 Projection 节点:
Aggregate: count(commits.id), groupby=users.name
└─Projection: [commits.id, users.name]
Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Projection: [users.id, users.name, repos.id]
│ Join: inner, on=true
│ ├─Projection: [users.id, users.name]
│ │ Scan: users [id, name, email]
│ └─Projection: [repos.id]
│ Filter: repos.name = 'RisingLight'
│ └─Projection: [repos.id, repos.name]
│ Scan: repos [id, name, url]
└─Projection: [commits.id, commits.user_id, commits.repo_id]
Filter: commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
└─Projection: [commits.id, commits.user_id, commits.repo_id, commits.time]
Scan: commits [id, user_id, repo_id, time, message]最后,我们可以将最下面的 Projection 与 Scan 算子合并,去掉 Scan 中不存在于 Projection 的列,执行列裁剪。另外,对于一些中间生成的 Projection,如果它们是恒等映射、并不具备裁剪效果,最后也可以被消除掉。在完整执行过投影下推和列裁剪之后,执行计划将变成这个样子:
Aggregate: count(commits.id), groupby=users.name
└─Projection: [commits.id, users.name]
Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Join: inner, on=true
│ ├─Scan: users [id, name]
│ └─Projection: [repos.id]
│ Filter: repos.name = 'RisingLight'
│ └─Scan: repos [id, name]
└─Projection: [commits.id, commits.user_id, commits.repo_id]
Filter: commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
└─Scan: commits [id, user_id, repo_id, time]与优化前的执行计划相比,新的计划避免了未使用的列被读取,还显著减少了 Join 算子输入输出的数据量。这些改进在 RisingLight 这种列存数据库中会起到非常明显的效果。
有了基本概念后,下面我们来讨论如何在 egg 中实现这些优化规则。
与上一节中的谓词下推相比,投影下推的实现更为复杂。原因是这里不再能使用 (and a b) 这样的简单操作来完成投影表达式的合并和过滤。我们首先考虑 Projection 下推 Filter 的情况,它的规则应该形如以下这样:
rewrite!("pushdown-proj-filter";
"(proj ?exprs (filter ?cond ?child))" =>
"(proj ?exprs (filter ?cond (proj ?new_exprs ?child)))"
),
其中 ?new_exprs 的位置应该是 ?exprs 和 ?cond 中所有列的并集组成的列表。例如:
?exprs = [$2.1]
?cond = (= $2.2 'RisingLight')
?new_exprs = [$2.1, $2.2]我们可以引入一个特殊节点来表达这种运算,比如就叫 (column-merge a b)。这样这条规则就可以完整地表示为:
rewrite!("pushdown-proj-filter";
"(proj ?exprs (filter ?cond ?child))" =>
"(proj ?exprs (filter ?cond (proj (column-merge ?exprs ?cond) ?child)))"
),
但是迟早我们还是要对 column-merge 进行“运算”,将其替换为一个 list 表达式。这个可以通过在 rewrite 中实现 egg 提供的 Applier trait 解决,它允许我们使用 Rust 自定义重写的内容和逻辑。首先我们定义这样一条重写规则:
rewrite!("column-merge";
"(column-merge ?a ?b)" =>
{ ColumnMerge { lists: [var("?a"), var("?b")] } }
),
然后定义名为 ColumnMerge 的结构体并实现 Applier trait:
/// 合并 `lists` 中所有节点的 Column 集合,并返回一个列表
struct ColumnMerge {
lists: [Var; 2],
}
impl Applier<Expr, ExprAnalysis> for ColumnMerge {
fn apply_one(&self, egraph: &mut EGraph, eclass: Id, subst: &Subst, ..) -> Vec<Id> {
// 分别提取 a 和 b 节点的 Column Analysis 结果
let a = &egraph[subst[self.lists[0]]].data.columns;
let b = &egraph[subst[self.lists[1]]].data.columns;
// 合并以上两个集合,并转化为 Id 的 List
let mut list: Vec<&ColumnRef> = a.union(b).collect();
list.sort_unstable();
let list = list.into_iter()
.map(|col| egraph.lookup(Expr::Column(col.clone())).unwrap())
.collect();
let id = egraph.add(Expr::List(list));
// 返回 List 节点作为结果
if egraph.union(eclass, id) { vec![eclass] } else { vec![] }
}
}
我们可以暂时忽略上述代码的实现细节,只需要知道:对于复杂的重写规则,我们都可以通过自定义 Applier 的方式在 Rust 中实现这些逻辑。从另一个角度看,我们是在 egg 的 DSL 中定义了一个“函数”叫 column-merge,利用它延迟求值的特性,组合出了更为复杂的规则。当时写到这里的时候,我就突然明白别人说的 Lisp 语言「代码即数据,数据即代码」是怎么一回事了。
以上我们通过定义 column-merge 节点实现了 Projection 对 Filter 的下推规则。对其它算子如 Limit / Order / TopN / Agg 的实现都大同小异。比较特殊的还剩 Scan 和 Join 算子。
对于 Scan 算子,我们需要用 Projection 中的集合对 Scan 的集合进行过滤。于是我们故技重施,定义一个新节点 (column-prune ?filter ?list),表示从 ?list 中删除没有在 ?filter 中出现过的元素。具体实现也不再赘述了,和上面的大同小异。有了它以后,我们对 Scan 算子进行列裁剪的规则可以定义如下:
rewrite!("pushdown-proj-scan";
"(proj ?exprs (scan ?table ?columns))" =>
"(proj ?exprs (scan ?table (column-prune ?exprs ?columns)))"
),
最后,对于 Join 算子,我们遇到了和谓词下推类似的问题:需要决定每个表达式下推 ↙?左边 还是 ↘?右边。恰好,这一需求也可以通过 column-prune 来实现:
rewrite!("pushdown-proj-join";
"(proj ?exprs (join ?type ?on ?left ?right))" =>
"(proj ?exprs (join ?type ?on
(proj (column-prune ?left (column-merge ?exprs ?on)) ?left)
(proj (column-prune ?right (column-merge ?exprs ?on)) ?right)
))"
),
我们首先用 (column-merge ?exprs ?on) 合并上面所使用的列,然后分别用左子树 ?left 和右子树 ?right 作为 ?filter 套一层 column-prune。这样就过滤掉了不属于自己这边的表达式。
整个投影下推和列裁剪的优化到这里就基本实现完了。不过还有最后一步要做,就是消除恒等的 Projection 算子。这一规则需要引入新的 Analysis 来分析每个算子输出的内容,我们放到下一篇「下标解析」一节中再讲。
鉴于上面的优化有些过于硬核,下面我们来讲一个简单点儿的放松一下:如何识别并将 Join 算子优化为 HashJoin。
朴素的连接,或者叫嵌套循环连接(Nested Loop Join),需要将左右两个表进行逐行处理,时间复杂度为 O(N * M)。而 HashJoin 则是当连接条件是多个等式情况下的一种优化。它首先从一侧读入整个表,并建立一个哈希索引;然后按顺序读入另一个表,对每一行查询哈希得到新的连接。它的时间复杂度为 O(N + M),通常远远优于朴素连接算法。考虑到实践中大部分的 Join 都满足转化为 HashJoin 的条件,因此这是一个必不可少的优化(否则数据规模稍大一点就跑不出来了)。
在上面的例子中:
Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Join: inner, on=true
│ ├─Scan: users ...
│ └─Scan: repos ...
└─Scan: commits ...就可以被优化为:
HashJoin: inner, on=([users.id, repos.id] = [commits.user_id, commits.repo_id])
├─Join: inner, on=true
│ ├─Scan: users ...
│ └─Scan: repos ...
└─Scan: commits ...我们要做的就是识别出这样的连接条件:l1=r1 AND l2=r2 AND …,
并从中提取出左边和右边的键:[l1, l2, …] 和 [r1, r2, …]。
这在 egg 中的实现也比较简单。我们首先定义 HashJoin 节点:
define_language! {
pub enum Expr {
"join" = Join([Id; 4]), // (join type condition left right)
"hashjoin" = HashJoin([Id; 5]), // (hashjoin type[left_expr..][right_expr..]left right)
// ...
}
}
与 Join 略有不同的是,它将连接条件中左右两边的键分开存放于两个列表中,以方便未来执行器的实现。
对于一个键的情况,我们有:
rewrite!("hash-join-on-one-eq";
"(join ?type (=?l1 ?r1) ?left ?right)" =>
"(hashjoin ?type (list ?l1) (list ?r1) ?left ?right)"
if columns_is_subset("?l1", "?left")
if columns_is_subset("?l2", "?right")
),
对于两个键的情况也是类似:
rewrite!("hash-join-on-two-eq";
"(join ?type (and (=?l1 ?r1) (=?l2 ?r2)) ?left ?right)" =>
"(hashjoin ?type (list ?l1 ?l2) (list ?r1 ?r2) ?left ?right)"
if columns_is_subset("?l1", "?left")
if columns_is_subset("?l2", "?left")
if columns_is_subset("?r1", "?right")
if columns_is_subset("?r2", "?right")
),
如果要实现对任意多个键的识别和转化,我暂时没想到像这样简单的写法,可能还是需要定制 Applier 才能做到。不过在实践中,通常键的数量也就是一两个,因此手动枚举规则也未尝不可。
除了优化连接算法以外,我们还可以调整多个连接的顺序,这一优化称为 Join Reordering。对于常用的内连接(Inner Join),它满足交换律和结合律。从执行计划树的角度来看,交换律相当于交换 Join 节点的左右子树,结合律相当于对二叉树进行旋转:
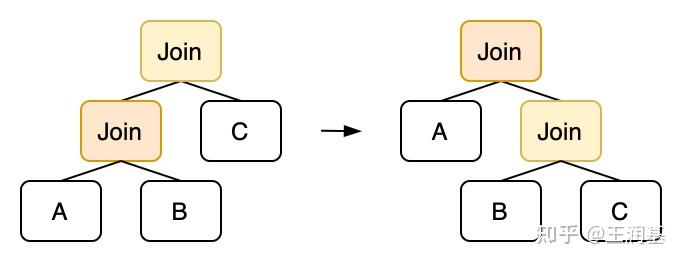
使用结合律,我们上面的三表连接 (users x repos) x commits :
Join: inner, on=(users.id = commits.user_id AND repos.id = commits.repo_id)
├─Join: inner, on=true
│ ├─Scan: users ...
│ └─Scan: repos ...
└─Scan: commits ...可以调整顺序为 users x (repos x commits):
Join: inner, on=(users.id = commits.user_id)
├─Scan: users ...
└─Join: inner, on=(repos.id = commits.repo_id)
├─Scan: repos ...
└─Scan: commits ...不同的连接顺序需要的执行开销可能截然不同。比如上面的执行计划就需要对 users 和 repos 两表做笛卡尔积,时空复杂度都是平方级别;而下面的执行计划中两个连接都可以被优化为 HashJoin,只需要线性的时空复杂度即可完成。
在 egg 中描述 Inner Join 的结合律也非常直观:
rewrite!("join-reorder";
"(join inner ?cond2 (join inner ?cond1 ?left ?mid) ?right)" =>
"(join inner ?cond1 ?left (join inner ?cond2 ?mid ?right))"
if columns_is_disjoint("?cond2", "?left")
),
其中 columns_is_disjoint(a, b) 函数表示:表达式 a 所使用的列和算子 b 所提供的列没有任何交集。因为如果外层的谓词包含左侧的列,那么它就不能被转到右侧去。当然这个规则有些保守了,我们完全可以先将两个谓词合并,然后提取出能够放到右边的谓词,这样规则就可以无条件执行。具体的写法就留给读者自己思考实现吧!(因为我也是刚想到这个问题(逃
同样的,我们还可以实现交换律:
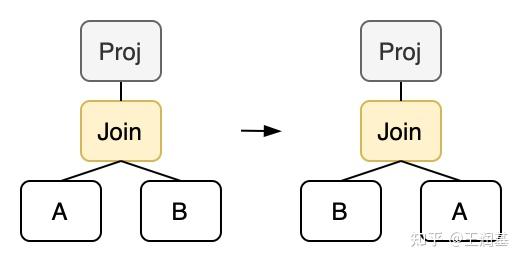
rewrite!("join-swap";
"(proj ?exprs (join inner ?cond ?left ?right))" =>
"(proj ?exprs (join inner ?cond ?right ?left))"
),
不过这里我们要求 Join 上面必须有一个 Projection 才能执行交换。因为交换左右子树会导致 Join 算子输出的列发生变化,这不符合我们对等价类的定义,严格来说交换后就不再是同一个 Join 节点了。如果强行交换的话,会导致后续 Schema 分析结果错乱。所以我们要在上面套一个 Projection,以保证重写前后两个算子的输出是完全一致的。在投影下推的配合下,我们可以保证 Projection-Join 这样的模式一定会出现。
使用上述两条规则,我们能够枚举出所有可能的连接顺序。对于 N 个表的连接,就存在着 N! 种不同的排列。在这么多方案中哪个是最优的呢?我们需要根据不同算法和数据规模进行估算才能知道。
在连接重排序之前,所有的优化规则都具有这样一个特点:我们知道变换后的形式一定比之前更优,因此可以直接替换掉之前的表达式。这些优化都属于 RBO(Rule-Based Optimization,基于规则的优化)。从连接重排序开始,我们就正式进入了 CBO(Cost-Based Optimization,基于代价的优化)的领域。它们的特点是:需要引入代价函数(Cost Function)来估算每种方案的开销,最终选择代价最小的一种执行。
由于 Equality Saturation 方法本身就是基于代价的,因此在 egg 中实现 CBO 易如反掌。我们只需在 CostFunction trait 下实现代价函数,然后扔给 egg 让它找出最优表达式即可。写成代码大概是这个样子:(完整代码可参考 RisingLight)
pub struct CostFn<'a> {
pub egraph: &'a EGraph,
}
impl egg::CostFunction<Expr> for CostFn<'_> {
type Cost = f32;
fn cost<C>(&mut self, enode: &Expr, mut costs: C) -> Self::Cost
where
C: FnMut(Id) -> Self::Cost,
{
use Expr::*;
// 定义一些辅助函数:
// rows: 估计算子输出的行数
// cols: 算子输出的列数
// out: 输出的数据量=rows * cols
// costs: 节点的总代价
match enode {
Scan(_) | Values(_) => out(),
Order([_, c]) => nlogn(rows(c)) + out() + costs(c),
Proj([exprs, c]) | Filter([exprs, c]) => costs(exprs) * rows(c) + out() + costs(c),
Agg([exprs, groupby, c]) => (costs(exprs) + costs(groupby)) * rows(c) + out() + costs(c),
Limit([_, _, c]) => out() + costs(c),
TopN([_, _, _, c]) => (rows(id) + 1.0).log2() * rows(c) + out() + costs(c),
Join([_, on, l, r]) => costs(on) * rows(l) * rows(r) + out() + costs(l) + costs(r),
HashJoin([_, _, _, l, r]) => (rows(l) + 1.0).log2() * (rows(l) + rows(r)) + out() + costs(l) + costs(r),
Insert([_, _, c]) | CopyTo([_, c]) => rows(c) * cols(c) + costs(c),
Empty(_) => 0.0,
// 对于其它表达式,设定代价为 0.1 x AST size
_ => enode.fold(0.1, |sum, id| sum + costs(&id)),
}
}
}
具体代价函数怎么设计还是挺有讲究的,需要多多调试才能让 egg 找到一个看上去合理的结果。我这里设计得还比较粗糙,但已经勉强能用了。它主要由几个部分构成:
out=rows x cols 的固定成本,这反映了输出时构建 DataChunk 的开销。rows x costs(expr)。这里面 rows 是对算子输出行数的估计,为此我们引入了一个新的 Analysis 来计算这个属性。
举几个例子:
false => 0.0 // 全部抛弃
true => 1.0 // 全部保留
(= id 1) => 1.0 / N // N 是总行数
(> age 50) => 0.2 // 根据实际数据分布得到的比例
(not (> age 50)) => 0.8 // 条件取反,概率也取反
(and (= id 1) (> age 50)) // 两个独立条件相交的 Selectivity 是二者的乘积
=> 0.2 / N // 当然这只是理想假设,实际数据可能有相关性更多知识请大家自行学习 CMU 15-445:)
具体代码就不放了,有兴趣可参考 RisingLight。目前 RisingLight 中对行数分析的实现并不完善。例如它对 Scan 返回的是固定行数,对条件表达式也是返回固定的 Selectivity,都没有用到存储数据的统计信息。这是一个很大的坑还没有填,如果大家有兴趣欢迎来 PR!
总之,现在我们有了代价函数,接下来就可以交给 egg 让它帮我们找到最优的执行计划了。整个搜索过程可以由 Runner 自动完成:
/// Optimize the given expression.
pub fn optimize(expr: &RecExpr) -> RecExpr {
// 给定初始表达式和重写规则,进行等价类扩展
let runner = egg::Runner::default()
.with_expr(&expr)
.run(&*rules::ALL_RULES);
// 给定代价函数,提取出最优表达式
let cost_fn = cost::CostFn {
egraph: &runner.egraph,
};
let extractor = egg::Extractor::new(&runner.egraph, cost_fn);
let (_cost, best_expr) = extractor.find_best(runner.roots[0]);
best_expr
}
不过,egg 的执行器现在还不太智能,它在重写表达式、扩展等价类的过程中并不会依据代价函数进行启发式搜索,而是暴力扩展出所有可能的表示。对于比较复杂的查询(例如 TPC-H 中常见的多表连接)很容易出现组合爆炸的情况。而一些特殊的重写规则(例如投影下推)可以被应用无数次,产生深度嵌套的表达式,更是助长了这种现象。
为了避免这一问题,我们对上述过程手动迭代多次,每轮迭代抽取出一个最优解作为下一轮的输入。相当于实现了半个启发式搜索。此外,我们还可以手动将规则划分为几类,进行多阶段优化,每个阶段只应用一部分规则。通过这些 workaround,我们的优化器已经可以在一定时间内(~100ms)将 TPC-H 查询优化到不错的结果了。(点击这里查看执行计划)
P.S. 以上链接中 RisingLight 的执行计划由 pretty-xmlish 优雅打印,感谢作者 @肥猪千里冰封 的强力支持!
这篇文章中我们使用 egg 实现了一个经典的 SQL 优化器。
我们从最简单的算子消除入手,依次探索了基于规则的谓词下推、投影下推和列裁剪优化,以及基于代价的连接重排序和 HashJoin 优化。
通过这些规则我们已经能够对常见的查询做到比较满意的优化。但是,要将这样一个优化器原型集成到实际的数据库系统中发挥作用,还有很多问题要解决。由于篇幅所限,我们放在下一篇文章中讨论这些问题,比如:
然后根据我的经验聊聊 egg 框架的好处以及仍待解决的问题。
最后,别忘了课后练习——去挑战一下 sql-optimizer-labs 哟!如果有任何问题或建议,欢迎到 GitHub 讨论区 留言!