凸优化中strongly convex和L-smooth有什么应用？

点击数：更新时间：2024-05-20 19:27:44

粗暴一点的看法的话：感觉就像，一上一下，强迫你的目标函数长得像一个二次函数.

如果是L-Lipschitz的，就有了一个二次函数的上界：

$f(x) \\leqslant f(x_0) + <\ abla f(x_0), x-x_0> + \\frac{L}{2}\\|x-x_0\\|^2 \\quad \\forall x$

如果是 $\\mu$ -strongly convex的，就有了一个二次函数的下界：

$f(x_0) + <\ abla f(x_0), x-x_0> + \\frac{\\mu}{2}\\|x-x_0\\|^2 \\leqslant f(x) \\quad \\forall x$

画个示意图，大概长这个样子：

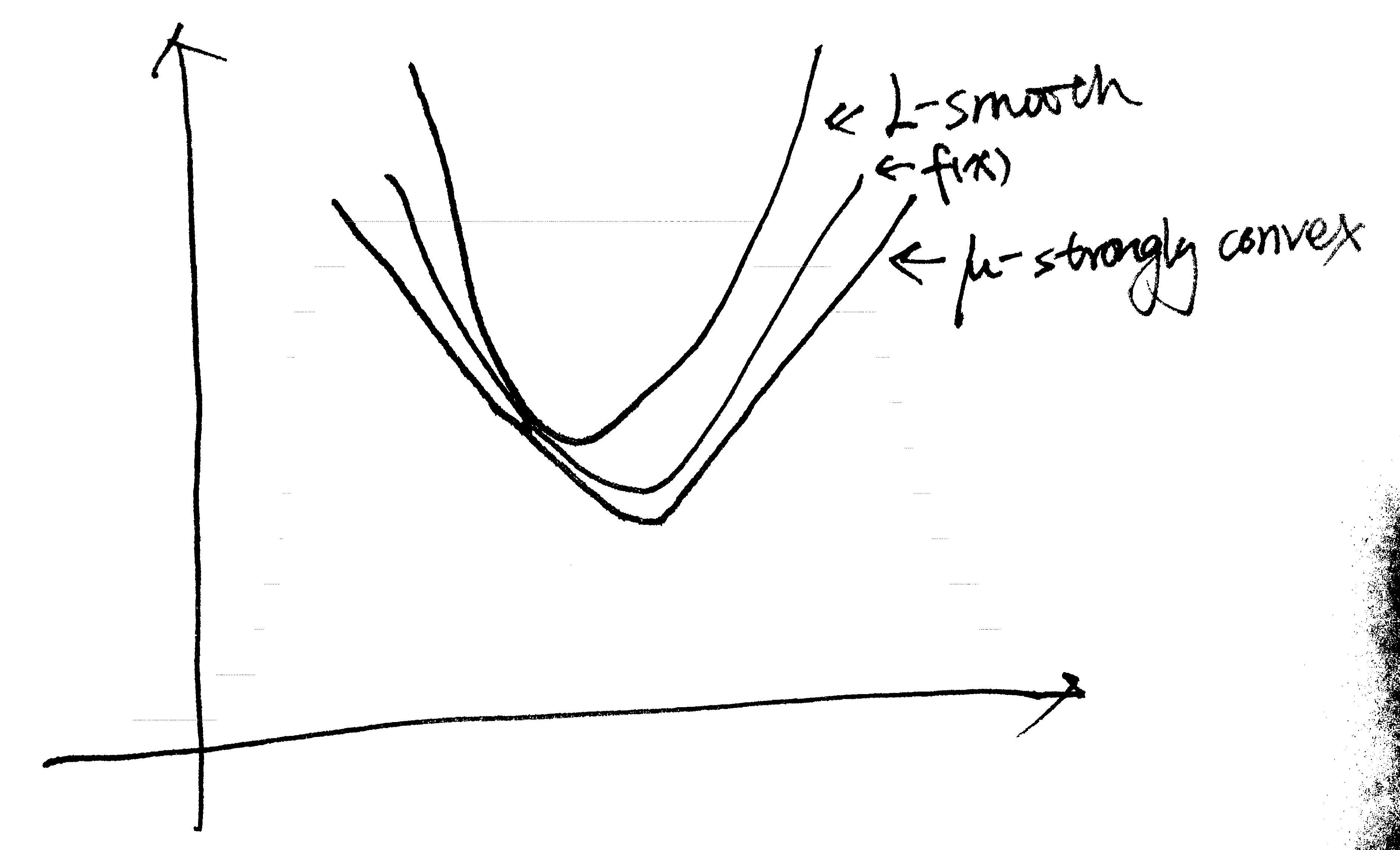
由于被迫长成一个二次函数的样子，于是很多算法在 $\\mu$ -strongly convex + L-Lipschiz下都有比较好的表现。

------------------------------------------------------------------------

最后欢迎关注我 @Zeap和我的专栏非凸优化学习之路哇，会写写关于nonconvex optimization的一些基本概念的介绍和自己的理解，希望对新手会有些帮助吧，里面的文章有：

Zeap：非凸优化基石：Lipschitz Condition

潘润琦：非凸优化的基石2：Regularity Condition

Zeap：当我们谈论收敛速度时，我们都在谈什么？

Zeap：如何理解非凸优化极值条件: 梯度=0 & 二阶导> 0？

证明收敛率需要这些条件，另外L-光滑和1/L-强凸有共轭对应关系。

$L$ -smooth中的 $L$ ，和 $m$ -strongly convex中的 $m$ 这一对CP，如果函数是二次可微的，可以认为它们就等同于函数Hessian矩阵的最大和最小奇异值的上界和下界，也就可以被看作梯度的最大变化速度和最小变化速度。由于SGD实在是一个短视的算法，每一步虽然也是在求解二阶近似，但都把Hessian暴力换成identity matrix了，这么说就明白了，梯度的变化率范围越小，在做GD step的时候越可控，由此反映在了GD的收敛性能上，具体可见这个答案～