拓扑排序详解通俗易懂

点击数：更新时间：2024-04-07 23:11:30

拓扑排序是对一个有向图构造拓扑序列，解决工程是否能顺利进行的问题。构造时有 2 种结果：

此图全部顶点被输出：说明说明图中无「环」存在，是 AOV 网
没有输出全部顶点：说明图中有「环」存在，不是 AOV 网

AOV（Activity On Vertex Network）：一种有向 无回路 的图

排序类似流程图一样任务

例如早上起床的任务：

例如：这里你只有穿了衬衣才能穿外套，而不是穿了外套再穿衬衣

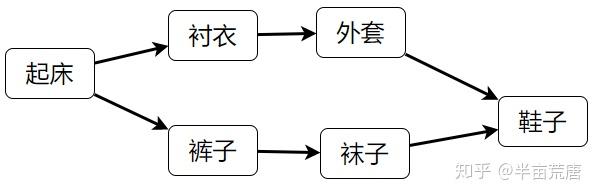
每次删除一个入度边个数为 0 的点，并刷新其他点的出度边个数。

对下面的图进行拓扑排序：

graph：使用领接表作为图的数据结构
stack：使用栈来储存入度边个数为 0 的点（减少每次查询入度边为 0 的边的计算）
inNumber：考虑到始终要计算入度边的数量，所以在来的 Vertex 顶点结构中增加 inNumber 来表示入度边的数量。

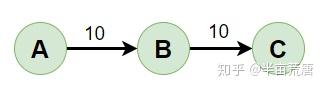
数据结构：

/** 边 */
static class Edge{
    /** 权重 */
    int weight;
    /** 出度指向的点 */
    int toVertex;
    /** 下一个出度边 */
    Edge next;
}
/** 顶点 */
static class Vertex{
    /** 入度 数量 */
    int inNumber;
    /** 顶点信息 */
    Character data;
    /** 第一条边 */
    Edge firstEdge;
}

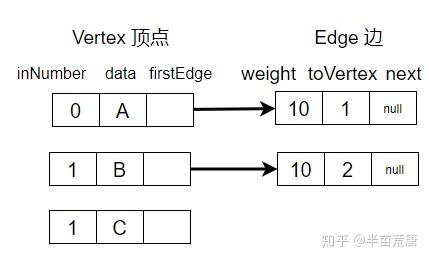
将所有入度边数为 0 的点放入 stack 栈中

（只有 A 入度边数为 0，将其放入栈中）

stack 中弹出 A 点
遍历 A 点的出度边并删除（只有 AB 一条出度边）
刷新其他点的入度边数：
B 点的入度边数量刷新为 0
判断 B 入度数量为 0 就入 stack 栈

stack 中弹出 B 点
遍历 B 点的出度边并删除（只有 BC 一条出度边）
刷新其他点的入度边数：
C 点的入度边数量刷新为 0
判断 C 入度数量为 0 就入 stack 栈

stack 中弹出 C 点
遍历 C 点的出度边并删除（C 没有出度边，所以无法刷新其他点的入度边数）
stack 栈中数据为空，程序结束

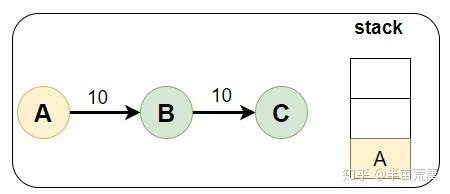
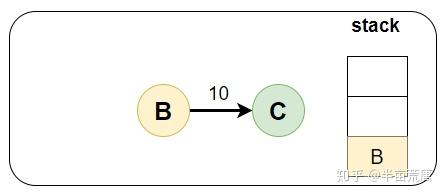
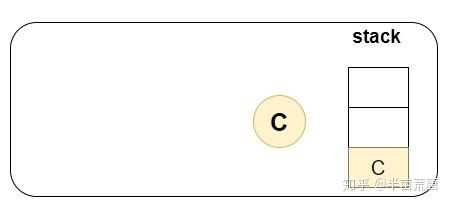
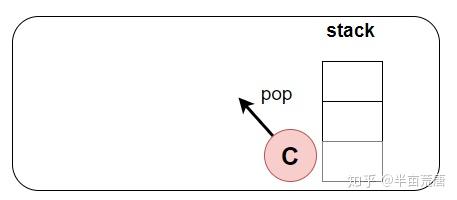
请结合代码理解图解案例分析

public class TopologicalSort {
    /** 边 */
    static class Edge{
        /** 权重 */
        int weight;
        /** 出度指向的点 */
        int toVertex;
        Edge next;
        public Edge(int weight, int toVertex, Edge next) {
            this.weight = weight;
            this.toVertex = toVertex;
            this.next = next;
        }
    }
    /** 顶点 */
    static class Vertex{
        /** 入度 数量 */
        int inNumber;
        /** 顶点信息 */
        Character data;
        /** 第一条边 */
        Edge firstEdge;

        public Vertex(int inNumber, Character data, Edge firstEdge) {
            this.inNumber = inNumber;
            this.data = data;
            this.firstEdge = firstEdge;
        }
    }
    /** 拓扑排序 */
    public static boolean topological(List<Vertex> graph){
        // 输出顶点的个数
        int outVertices = 0;
        // 栈：用来储存入度个数为 0 的顶点
        Stack<Vertex> stack = new Stack<>();
        //将顶点入度个数为 0 的元素入栈
        for (Vertex vertex : graph) {
            if (vertex.inNumber == 0) {
                stack.push(vertex);
            }
        }
        // 直到 AOV 网中不存在入度为 0 的点 
        while (!stack.empty()){
            // 弹出顶点
            Vertex pop = stack.pop();
            // 输出弹出的顶点
            System.out.println(pop.data);
            // 统计输出个数
            outVertices ++;
            //遍历这个点的出度
            Edge outEdge = pop.firstEdge;
            while (outEdge!=null){
                //出度的目标入度减少
                Vertex toVertex = graph.get(outEdge.toVertex);
                toVertex.inNumber --;
                //目标减少后 入度为 0 就入栈
                if (toVertex.inNumber == 0){
                    stack.push(toVertex);
                }
                outEdge = outEdge.next;
            }

        }
        // 输出所有点才返回 true.
        if (outVertices == graph.size()){
            return true;
        }
        return false;
    }
        /** 测试 */
    public static void main(String[] args) {
        //构建图 A -> B -> C
        ArrayList<Vertex> graph = new ArrayList<>();
        //环 测试
//        Edge edge1=new Edge(10, 1,null);
//        Edge edge2=new Edge(10, 2,null);
//        Edge edge3=new Edge(10, 0,null);
//        Vertex a=new Vertex(1, 'A', edge1);
//        Vertex b=new Vertex(1, 'B', edge2);
//        Vertex c=new Vertex(1, 'C', edge3);
        //无环 测试
        Edge edge1 = new Edge(10, 1,null);
        Edge edge2 = new Edge(10, 2,null);
        Vertex a = new Vertex(0, 'A', edge1);
        Vertex b = new Vertex(1, 'B', edge2);
        Vertex c = new Vertex(1, 'C', null);
        graph.add(a);
        graph.add(b);
        graph.add(c);
        //判断是否拓扑
        System.out.println(topological(graph));
    }
}