0898-08980898 13876453617
有没什么简单的描述?
简单讲就是因为拓扑效应引起的缺陷,在同伦意义下总是存在缺陷的。
比如说这个体系存在某种对称群,对称性破缺后会有与这个破缺的对称性相对应的真空(基态)。从一个真空到另一个真空存在一种能量极低的过渡态,这种一般被成为soliton,就是一种拓扑缺陷,例子是铁磁体系的磁筹,因为他两端对应的都是良好铁磁相,但是m的方向不同,是两个不同的真空。
再比如,欧式空间中,存在一种激发,使得矢量场在r->\\infty 并固定r时会给出位置r(是个球面)到矢量场方向(也是个球面)的一个映射。这个映射可以是不平凡的,但是欧式空间本身同伦于一个点,因此,如果这个映射良好定义,这个映射一定是平凡的,矛盾了。所以要求空间某个点这映射一定不能良好定义,也就是矢量等于0。所以空间中一定存在一个场量为0的缺陷点。这种叫做instanton。也是种拓扑缺陷。类似还有skyrmion。。。等
对称破缺后的真空流形可以做拓扑“”分类”, i.e. 不同阶的同伦群。如果存在拓朴非平庸的解,一般就意味着存在拓扑缺陷。比如说,3D的系统,二阶同伦群为Z,就说明存在hedgehog这样的缺陷,通俗的说,就是存在一个“点”(hard core,length scale一般是相干长度),上的序参量不在真空流形上。
但是,skyrmion却又比较特别,得用relative homotopy group。而且序参量往往在真空流形上(假设系统只经历一次对称破缺,且不考虑aproximate symmetry,i.e.液氦3中的SO(3)*SO(3)),存在的是soft core。
常见的就是,孤子,渦旋,斯格明子。
拓扑缺陷是什么?拓扑缺陷,它的一般特征是核心区域的结构被破坏,远离核心区域的结构缓慢变化。我们称之为“拓扑”缺陷的原因是它无法通过连续变化消失。
我们通过同伦理论对拓扑缺陷分类。以下例子是二维空间中的二维自旋。首先需要定义序参量的数值 。
例如二维系统中设定 ,其中
是一个常数,
有极坐标
。注意到原点处因为
存在奇点,我们可以设定原点处
。围绕缺陷核转一圈,角度
增加
,
为整数,被称为绕数(winding number)。例如下图:
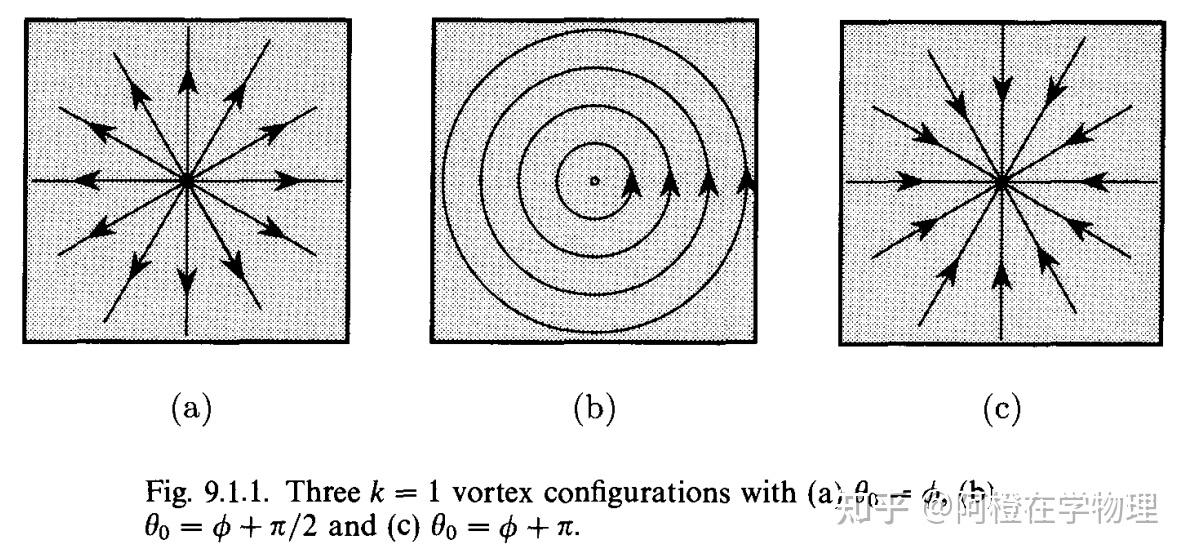
从同伦(homotopy)理论解释是:因为现在自旋是在二维面内,我们描述它只需要它的方向,对应的序空间就是一个圆环。现在讲时空间围绕缺陷的自旋映射到序空间上,可以想象将实空间的轮廓“缩”到一个圆环上, 表示在圆环上绕的圈数和方向,下图是
的例子。
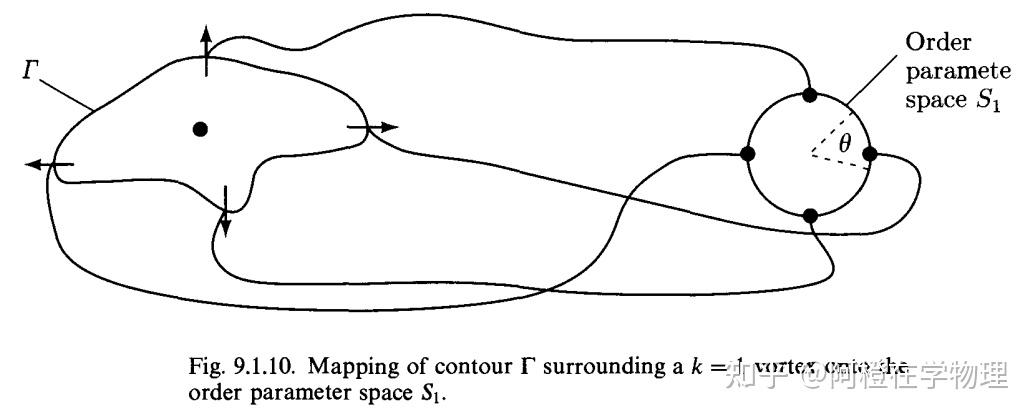
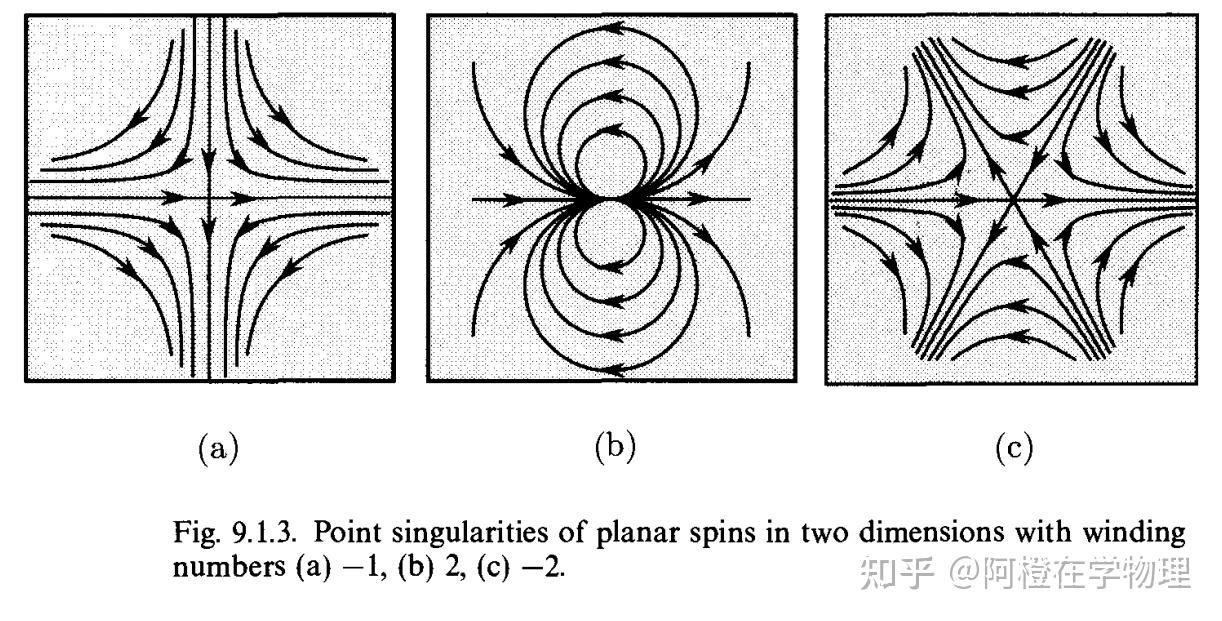
不同则对应不同的拓扑类,不能通过连续形变相互转化。
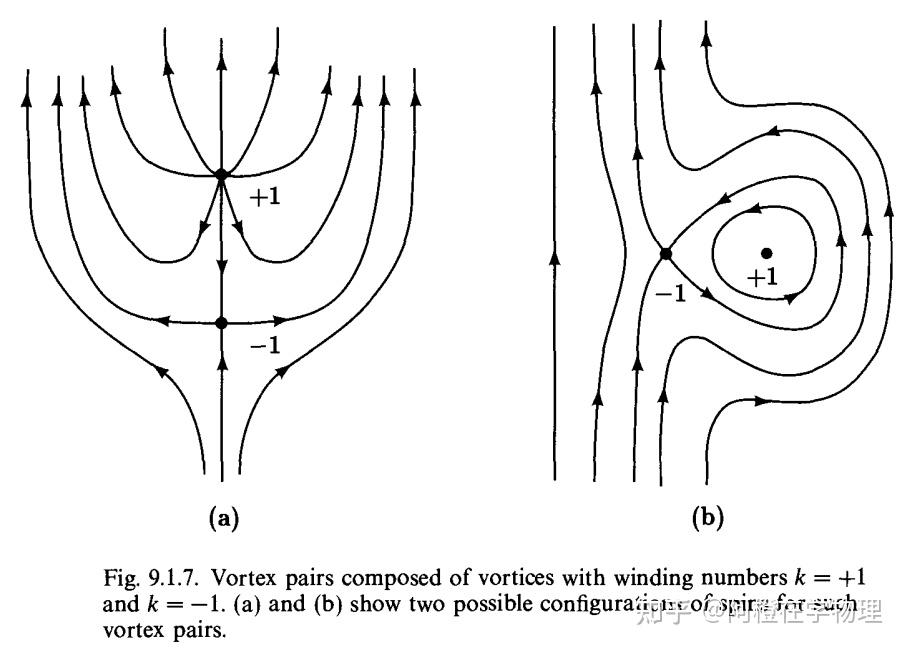
一对k相反的漩涡(下图)可以连续地变换到一起消失,所以它们拓扑等价于没有漩涡地均匀态。如果我们围绕这一对漩涡映射到序空间,可以看到k=0.
参考于:
书籍Chaikin - Principles of Condensed Matter Physics-Cambridge University Press 2000
第九章Topological defects (拓扑缺陷)
9.1 Characterization of topological defects