0898-08980898 13876453617
1 路径规划和轨迹优化的方法概括
基于搜索的路径规划有两项,分别是Dijkstra和A*算法;
基于采样的路径规划有三项,分别是RRT、RRT*和Informed RRT*算法;
基于智能算法的路径规划两项,分别是遗传算法和蚁群算法。
轨迹表示方法有两种方法,分别是多项式曲线和贝塞尔曲线;
轨迹优化目标有两种方法,分别是最小化snap和轨迹长度;
轨迹约束有两种方法,分别是软约束和硬约束。
2 路径规划算法详解
从起点开始逐步扩展,每一步为一个节点找到最短路径。Dijkstra的核心思想是贪心算法的思想。贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。在网上有看过这样一个对贪心算法的比方,就是当我们去吃自助餐,我们的目标是吃回本钱,但是我们的胃是有限的,所以我们的策略是每次吃最贵的食物。
在这个Dijkstra算法课程的流程的核心很简单,只需要两个列表,一个是open list(存放的是已经更新过的从其他节点到初始节点有路径的节点),另一个是closed list(存放的是收录以后的节点,已经找到了前往起点最短路径的节点)。即我们首先将起点放入open list当中,将open list当中f(n)最小节点放入到closed list当中,检查closed list中的节点为我们需要的节点,则找到最佳路径,但是如果没有,则需要遍历当前节点末在closed list中的邻接节点,如果节点在open list当中,则更新节点f(n)的值,否则计算节点f(n)的值,加入到open list当中。以此为循环,如果在closed list当中找到了目标节点的值,则找到最优路径,退出程序。
2.2 Dijkstra算法习题思考
在这里有一个练习题可以很好解释Dijkstra算法是如何寻找最优路径的,如图1所示,使用Dijkstra算法的情况通常都是要在栅格地图中进行,所以在论文中也经常会见到构型空间(Configuration Space)。

图1.Dijkstra算法习题
首先我们处于起点,第一步我们站在起点上向外看周围的节点,找一个距离离我们最近的节点,所以closed list此时有两个节点,分别是1(0)和4(1),因为我们要遍历周围的每一个节点,所以在open list中存了2(2)这一个节点,此时从起点向外延伸的两个节点我们都走到了,但是在open list中比较4(1)<2(2),所以将4(1)存入到了closed list中进行储存。根据前面所描述的算法,我们下一步就要遍历4和2节点周围的节点,我们先走4节点,发现4节点周围有三个节点分别是3、6和7,此时我们计算一下从1经过4再到3、6和7这三个节点的距离,分别是3(3)、6(9)和7(5),相比于这三个节点,则2(2)更短,于是将2(2)放入closed list当中。接着我们需要从2节点向外看,发现有4和5节点,但是4我们走过了,所以我们从1到2到5,计算出来5(13)节点并放入open list中。当我们遍历完4和2节点后,接着就是遍历3、6、7和5节点,从3节点上向外看,有1和6节点,因为1节点是起点,所以我们不走,于是我们走6号节点,这是我们第一次到达终点,即目标点。此时我们在open list中更新了6(8),即从1到4到3到6,比较路径长短后,将3(3)存入closed list中,因为6是终点所以6不走,最后从7节点遍历其他节点,发现只有6,则又规划出了一条从1到4到7到6的路径,计算出6(6),最终在open list当中比较更新出一条到达6的最短路径。至于5节点,它处于7节点的后面,并且5(13)远大于7(5),所以不需要计算考虑。
综上所述,将Dijkstra算法总结为两句话,记为从未访问的节点选择最小距离的节点进行收录,即贪心思想,之后从收录节点后遍历该节点的邻接节点,并更新,重复以上过程直到找到最优路径。
2.3 Dijkstra算法的优缺点
首先从上面的习题中,我们就可以看到该算法的优点就是可靠,因为它遍历了栅格地图中的每一个节点,并从中选择出一条最优的路径,所以我们可以相信这条路径在此刻看来是最优路径。但是缺点也很明显,首先该算法必须要在有栅格的地图中才可以进行,但是基本上所有的地图都是不带有网格的,因此我们要使用这个方法,第一步就是要进行网格的划分,问题也随之而来,如何确保我们选择的网格大小就是最后能形成最优路径的网格大小,所以我们不能找到最优的网格大小和密度,我们只能通过经验来估算,就这一点也是Dijkstra算法最大的缺点。其次Dijkstra算法需要遍历每一个节点,并且还要计算邻接节点到起点的路径,进行更新,所以这个计算量是很大的,大的计算量对应的是冗余的算力和长时间的计算,这是第二大缺点。因此为了减少计算和降低计算时长,有了第二种算法为A*算法。
2.4 A*算法
A*算法提出的动机是为了减少收录栅格的数量,从而减少搜索时间,因为A*算法是基于Dijkstra算法的,所以算法的主体不变,只需要每次在open list选取最小节点时加入启发式函数F(n)=f(n)+h(n),这样在选取临近节点时,加一个函数值约束,直接选取最优点,而可以不用去遍历其他节点浪费时间,最终两个算法的效果图如图2所示。
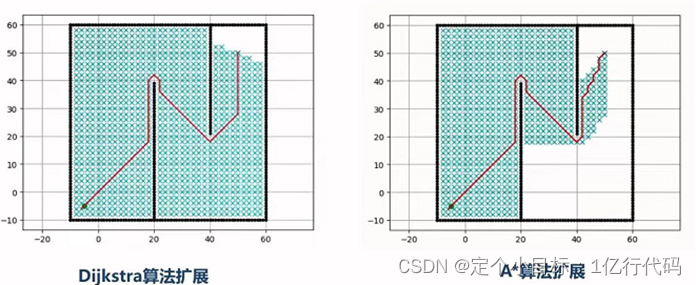
图2.基于搜索的路径规划两种方法对比
我们可以看出Dijkstra算法和A*算法的区别,虽然A*算法大大加快了计算速度,但是在前面提到的Dijkstra算法中第一个缺点,即基于搜索的路径规划算法必须要在具有网格节点的地图中进行,所以划分网格空间成为了该种路径规划算法的最大缺点。
2.5 RRT算法
起点作为一颗种子,从它开始生长枝丫;在机器人的“构型”空间中,生成一个随机点;在树上找到距离最近的那个点,记为a;朝着a的方向生长,如果没有碰到障碍物就把生长后的树枝和端点添加到树上,返回true。
随机点一般是均匀分布的,所以没有障碍物时树会近似均匀地向各个方向生长,这样可以快速探索空间。当然如果可以事先掌握最有可能发现路径的区域信息,可以集中兵力重点探索这个区域,这时就不宜用均匀分布了。
其中有几个要注意的点在这个算法中:
2.6 对于RRT算法的改进想法(融入了RL思想)

图3.RRT算法中障碍物地图
因为我们知道智能体本身是具有一定大小体积的,为了能更好地通过障碍物到达目标点,我们需要智能体与障碍物之间形成一定的安全距离,如图3所示。所以我将RL思想中reward的奖惩机制引入到这里,可以设定一个标准,如果轨迹距离圆心的距离小于等于障碍圆的半径,则得到-1分,如果轨迹距离圆心的距离大于障碍圆的半径但小于(障碍圆半径+智能体圆半径)/f(x),我设这里的f(x)为一激励函数,当0<f(x)的值<1时,则在每一个episode中得到-f(x)值,当1<f(x)的值时,则在每一个episode中得到-1/f(x)值。如果轨迹距离圆心的距离大于(障碍圆半径+智能体圆半径)/f(x),则得到1分。最终比较所有episode的值,选出最大正数,即最安全路径。
另一个点就是如何计算轨迹到障碍物之间的距离,这里直接使用点到直线的距离,通过向量矩阵的运算即可求得,求得后再减去障碍物半径得到最终结果。
2.7 RRT算法的优缺点
首先我们对比Dijkstra算法和A*算法,RRT算法不需要进行网格空间的划分,增强了随机化的概念。但是RRT算法的缺点也很明显,因为步长的限制,它无法寻找到一条最优路径,只能尽量避开障碍物,这无法满足最短路径的需要。因此我们引出了RRT*算法。
2.8 RRT*算法
如我们前面所描述的RRT算法是一个相对高效率,同时可以较好的处理带有非完整约束的路径规划问题的算法,并且在很多方面有很大的优势,但是RRT算法并不能保证所得出的可行路径是相对优化的。因此许多关于RRT算法的改进也致力于解决路径优化的问题,RRT*算法就是其中一个。RRT*算法的主要特征是能快速的找出初始路径,之后随着采样点的增加,不断地进行优化直到找到目标点或者达到设定的最大循环次数。RRT*算法是渐进优化的,也就是随着迭代次数的增加,得出的路径是越来越优化的,而且永远不可能在有限的时间中得出最优的路径。因此换句话说,要想得出相对满意的优化路径,是需要一定的运算时间的。所以RRT*算法的收敛时间是一个比较突出的研究问题。但不可否认的是,RRT*算法计算出的路径的代价相比RRT来说减小了不少。RRT*算法与RRT算法的区别主要在于两个针对新节点xnew的重计算过程,分别为:重新为xnew选择父节点的过程, 比起RRT多了一个rewire的过程;重布线随机树的过程。
RRT*算法的核心在于在局部面积的路径中寻找父节点,由父节点来判断是形成新路线还是保持原路线,所以该路径是局部渐进迭代的结果。对比RRT算法,RRT*算法的确可以找出一条渐进最优的路径,但是多次迭代所需要的时间也是该算法的缺点。
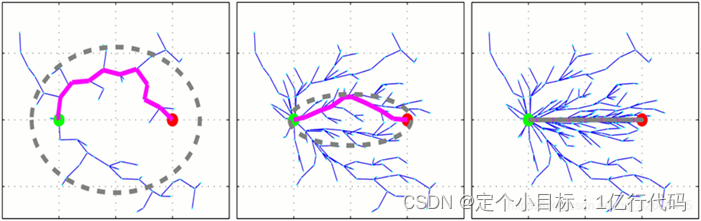
图4.椭圆空间压缩过程
 ?
?
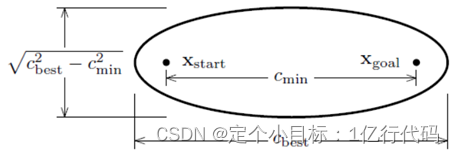
图5.椭圆大小
该方法是采样点函数改进,每次要在椭圆里采样。首先要求解出Cmin,接着要求出Xcentre,Xcentre位于椭圆的中心点。因为路径角度的不同就形成了不同角度的椭圆,所以就形成了与世界坐标角度不同的坐标系,这个时候就需要求椭圆坐标和世界坐标之间的旋转矩阵,课程中提到了一个Kabsch算法来求解旋转矩阵。将不同维度的r依次存入到对角矩阵L中。因为我们先是在圆里面进行采样的,所以提前设了一个Xball,给Xball乘以一个维度压缩的对角矩阵L,再乘以一个旋转矩阵C,最后加一个平移的位移就可以得到我们想要的椭圆区域。话句话说,相当于把圆压扁拉长得到椭圆。
2.10 基于遗传算法的路径规划

图6.遗传算法规划图
遗传算法的核心可以总结为“模拟生物进化过程,物竞天择,适者生存”,首先是种群的初始化,(1)在每行选择一个栅格(2)判断相邻栅格是否连续(3)不连续时进行插入栅格操作,直到其连续。下一步就是选择的过程,类比为我们平时的圆盘抽奖,好的个体面积大,被选中的概率就大,反之亦然,但是我们仍保留个别坏的个体,因为它们可能会在后续的交叉和变异中变成非常好的选择。交叉即路径之间交叉,两个交叉的路径就会形成两个新的路径。而变异则是在网格中随机选择路径中的两个栅格,并采用种群初始化的方法在两个栅格间产生新的路径。最后我们只需要不断循环选择、交叉和变异操作,保留下最优路径即可。
关注博主,后续还会更新轨迹优化的知识总结!!!