0898-08980898 13876453617
0898-08980898 13876453617
目录
2、使用上述过程的最佳算法，对不同规模的f(x)求解。 10
优化问题在很多领域有着重要的应用，本次报告通过不同的算法对不同规模的进行最优化求解（本次所有计算程序均用Python编写）。
这显然是一个无约束优化问题。
通过迭代次数与算法运行时间,比较算法的优劣。
1.1、梯度下降法
迭代格式为：
梯度下降法非常简单，只需要知道如何计算目标函数的梯度就可以写出迭代格式。因此，尽管在不少情况下梯度下降法的收敛速度都很慢，也依然不影响它在工业界的广泛应用。因此问题就变成不同步长的选取了。
下面分别根据准则对步长进行选取最优化的梯度下降法。
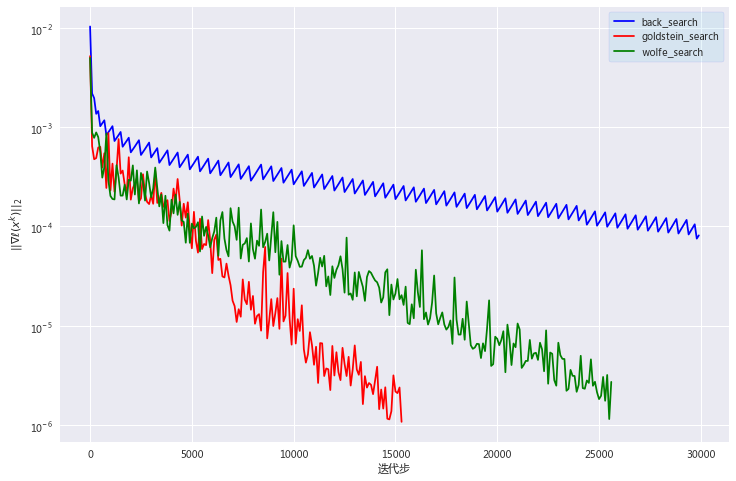
以上最优解为：
梯度下降法goldstein_search运行了:16.528993844985962s
梯度下降法goldstein_search迭代了：15371 次
梯度下降法goldstein_search最优解的函数值为：5.0041385560012e-10
从上图可知，梯度下降法的迭代次数都在1.5w步以上。Goldstein准则收敛速度最快，回退法收敛速度最慢。
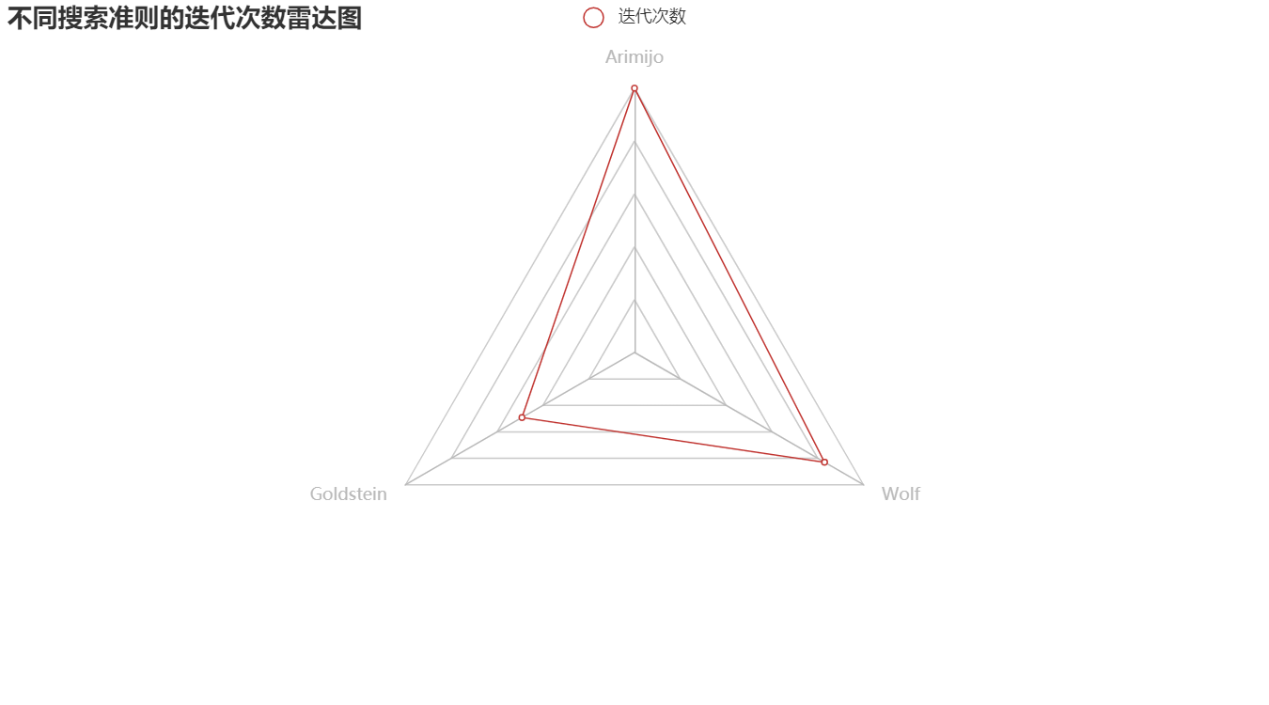
在迭代次数上，Goldstein<Wolf<back_search，Goldsetin法效果最佳。
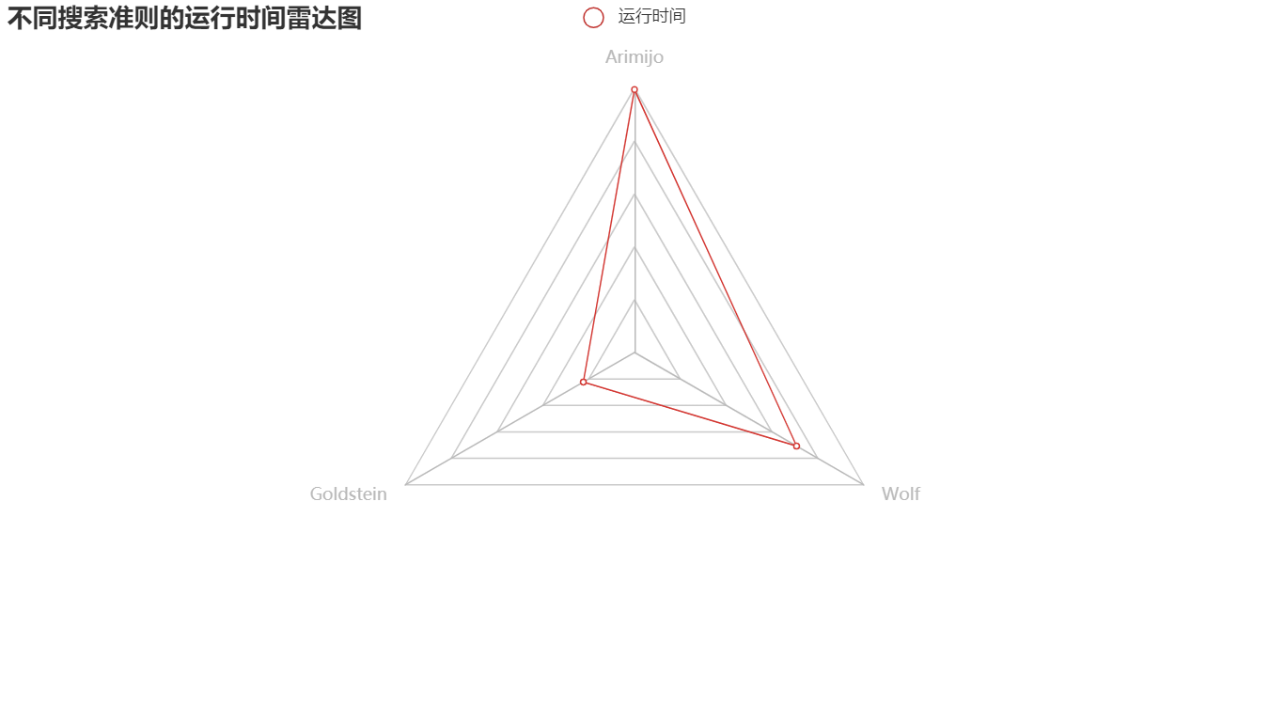
在运行时间上，Goldstein<Wolf<back_search，Goldsetin法效果最佳。
综上，梯度下降法，最佳的搜索准则为Goldsetin准则，最佳迭代次数为14754次，最佳运行时间为16.76125693321228s，最优解的函数值为：2.2527475430002451e-10。可见，梯度下降法效果一般，收敛速度太慢，下面跟进其他算法。
Barzilar-Borwein (BB)方法是一种特殊的梯度法，经常比一般的梯度法有着更好的效果．从形式上来看，BB方法的下降方向仍是点xk处的负梯度方向，但步长αk并不是直接由线搜索算法给出的．考虑梯度下降法的格式:,
这种格式也可以写成,其中．BB方法选取的是如下两个最优问题之一的解:
对使用BB方法进行最优化求解：
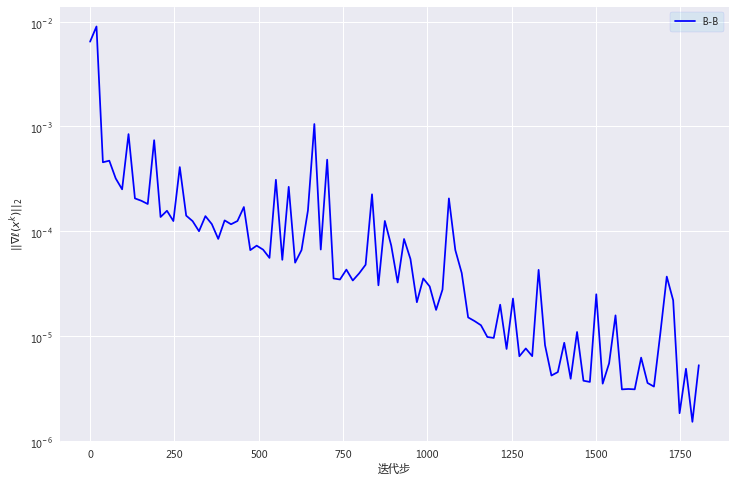
以上最优解为：
BB算法运行了:0.7366065979003906s
BB算法迭代了：1811 次
BB算法最优解的函数值为：8.08401664500936e-12
可见，BB方法在运行时间、迭代次数、最优解的精度上都远远胜于上述的梯度下降法。BB方法用更少的时间，得到了更优的解。
梯度下降法的下降方向为梯度的反方向，但这只是一个局部最优解。而共轭梯度法，很好的克服了这个局限性，从全局的角度出发，寻找最佳下降方向。
下面分别在共轭梯度法下，根据准则对步长进行选取，进行最优化。
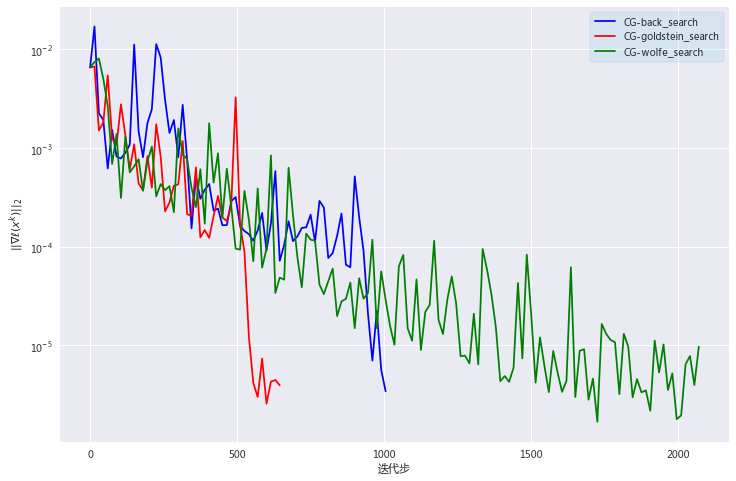
经过多次实验，这在共轭梯度下的三种搜索方法，迭代次数的随机扰动有点大，但大部分迭代次数都在次之间。
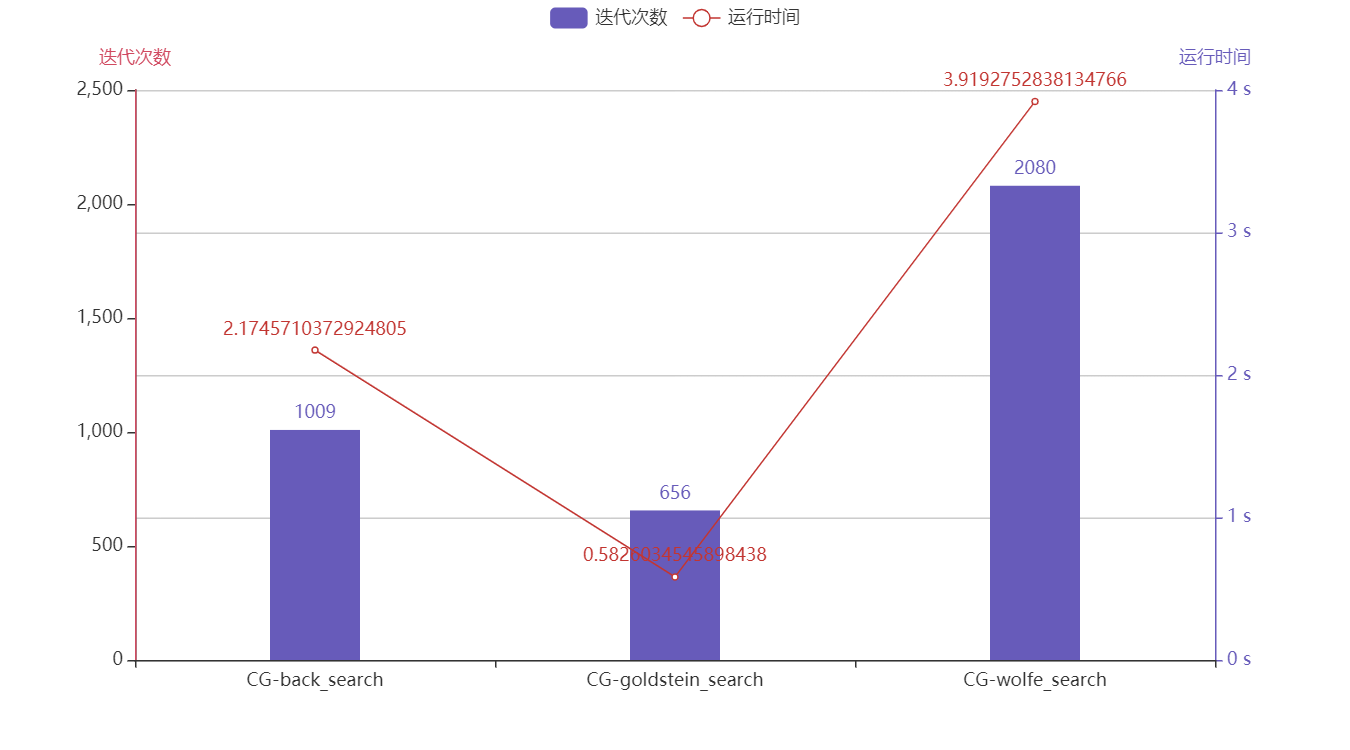
以上最优解为：
共轭梯度法goldstein_search运行了0.5826034545898438s
共轭梯度法goldstein_search迭代了656次
共轭梯度法goldstein_search最优解的函数值为4.0438514047321846e-11
可见，共轭梯度法进一步减少了迭代次数，缩短了运行时间，极大提高了最优化的效率。
BB方法与共轭梯度法都取得了不错的效果，那么和自然的想把他们结合在一起试试实际效果。下降方向选为共轭方法，步长搜索选为BB方法。
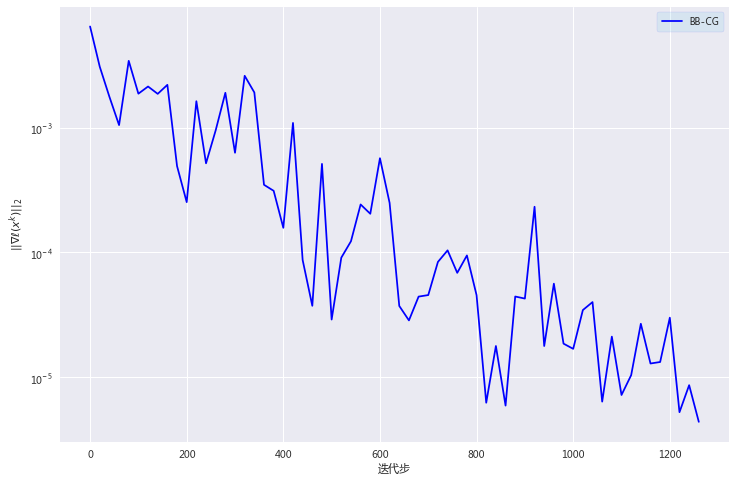
以上6最优解为：
BB-CG算法运行了:1.0713152885437012s
BB-CG算法迭代了：1268 次
BB-CG算法最优解的函数值为：1.1395745923571703e-10
不知道什么原因，BB-CG算法效果没有共轭梯度法好，但差别不太大，可能是我参数没有设好。
以上算法都只用了一阶导数的信息，应该向利用二阶导数信息发展。而由于这个函数我无法算出其二阶导数，所以只能取二阶导数的近似矩阵，即拟牛顿法。拟牛顿法虽然克服了计算海瑟矩阵的困难，但是它仍然无法应用在大规模优化问题上．一般来说，拟牛顿矩阵或是稠密矩阵，而存储稠密矩阵要消耗的内存，这对于大规模问题显然是不可能实现的．而有限内存BFGS方法（L-BFGS）解决了这一存储问题，从而使得人们在大规模问题上也可应用拟牛顿类方法加速迭代的收敛。下面介绍L-BFGS算法在最优化的过程。
分别用内置的Wolf1、Wolf2、Armijo准则对步长进行搜索：
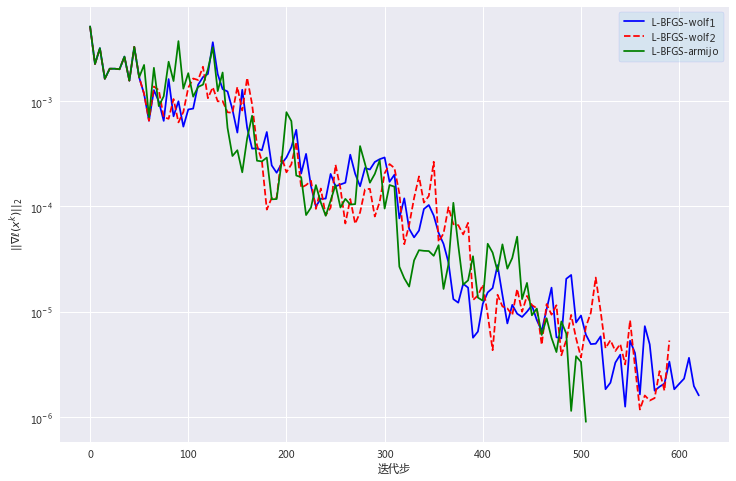
最优算法为L-BFGS-armijo，迭代次数为506次，运行时间 为0.5516269207000732s，最优解为5.659463100514601e-12。
得到各算法的迭代次数与运行时间对比图
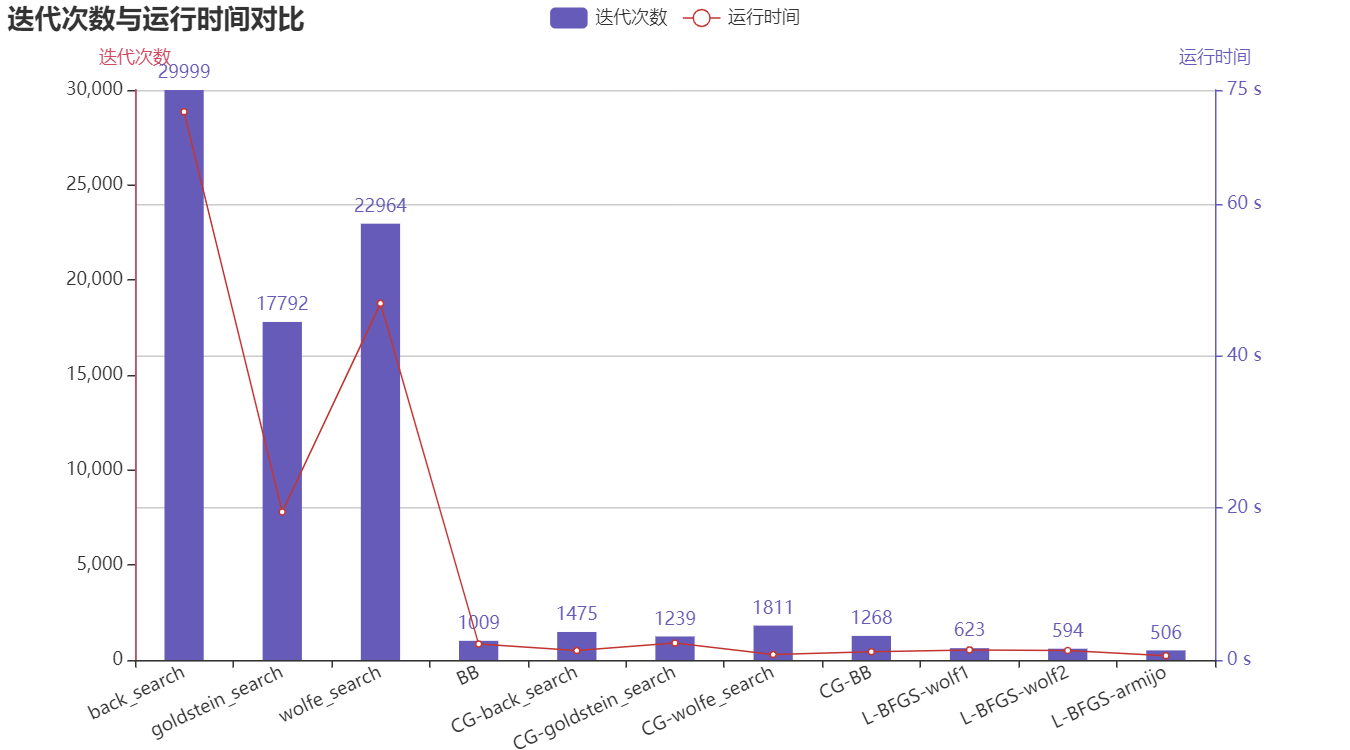
可得，最佳算法为L-BFGS-armijo算法。利用了二阶导数的拟牛顿法更加占据优势，明显由于前面的算法。
L-FBGS方法-armijo运行了0.5427207946777344s
L-FBGS方法-armijo迭代了506次
L-FBGS方法-armijo最优解的函数值为5.659463100514601e-12
选取最佳的L-FBGS方法-armijo算法对不同规模的进行求解。
取进行最优化运算。
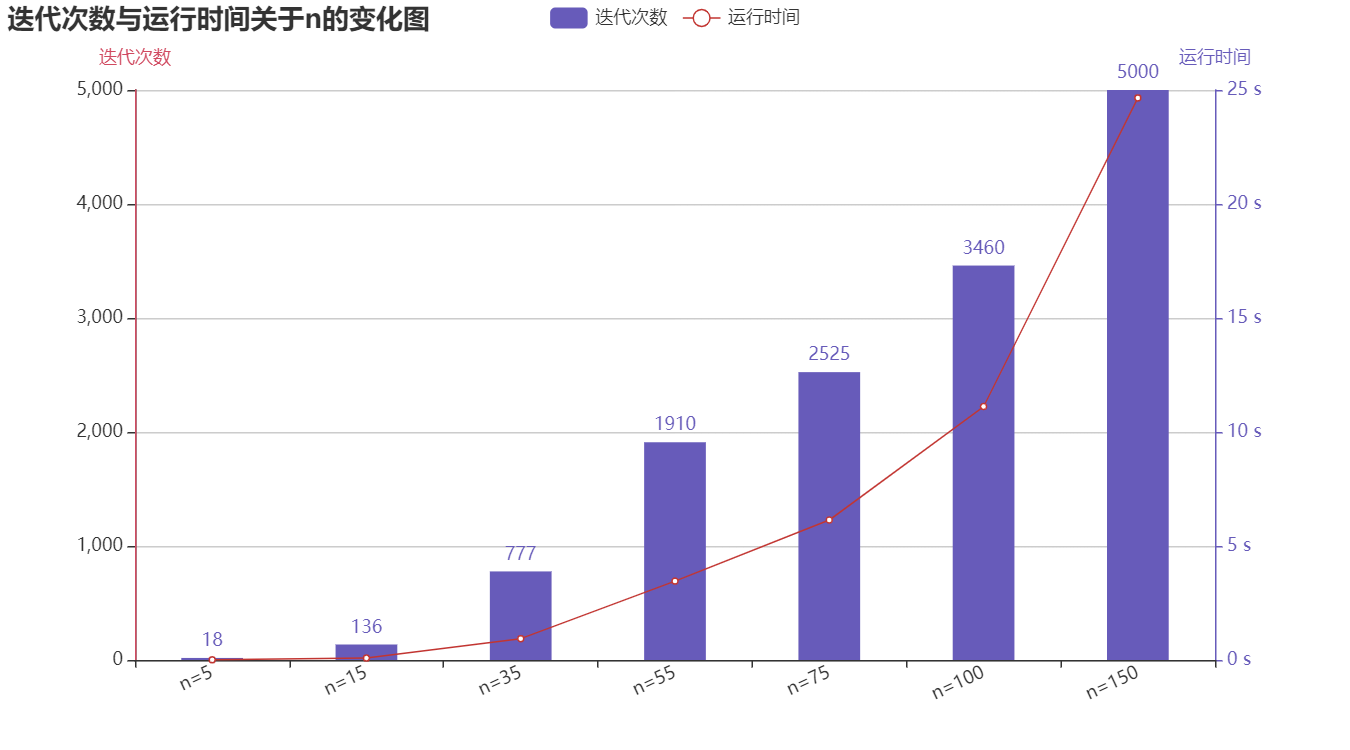
当等很小值时，L-FBGS方法-armijo算法能很快得通过很少的迭代次数找到最优解。但当时，面对巨大的维度，L-FBGS方法-armijo算法仍然能较好的解决问题。当,能以5000次迭代次数，24.65s的速度完成最优化，相对来说，还是能比较快速的完成最优化f(x)。
以上6次迭代最佳值;
初始点5,L-FBGS方法-armijo运行了0.5364747047424316s
初始点5,L-FBGS方法-armijo迭代了491次
初始点5,L-FBGS方法-armijo最优解的函数值为4.003781162312203e-11
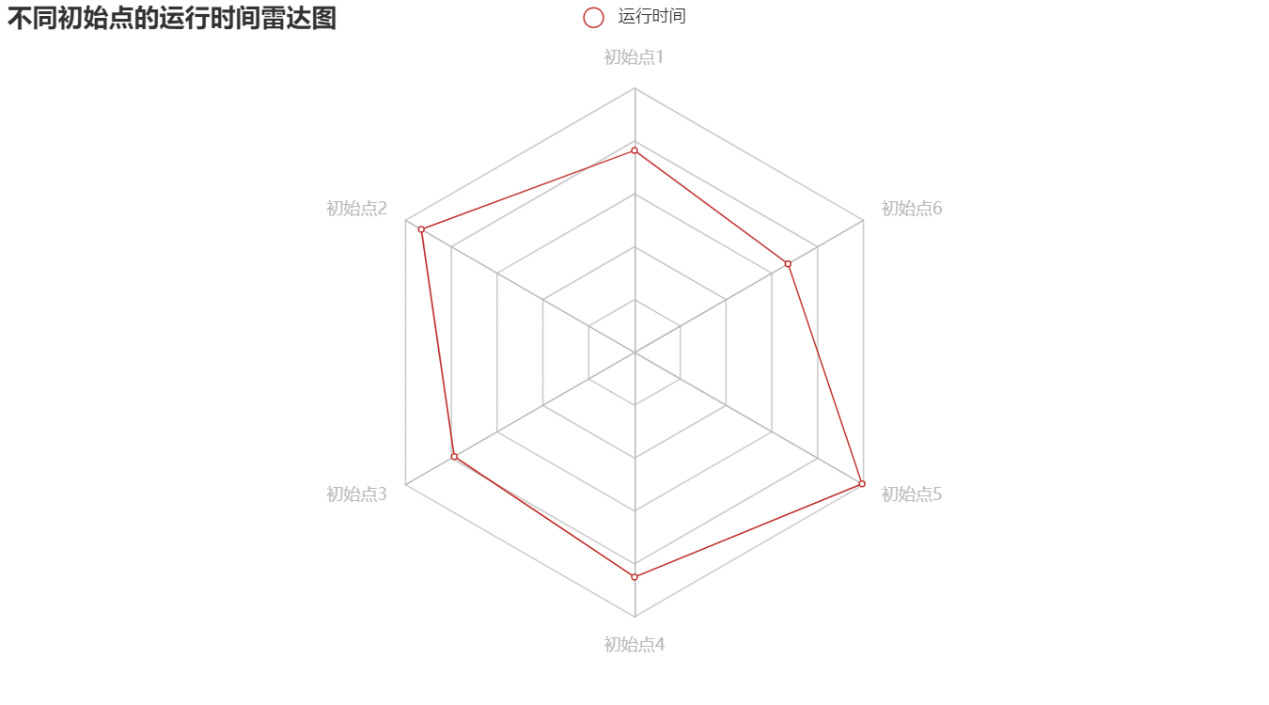
可以看出，当各维度的值都接近在0-1之间时，从不同初始点，L-FBGS方法-armijo算法的迭代次数与运行时间相差不大，最后都能找到近似最优解，受不同初始点的扰动很小，而且运行时间都很快。
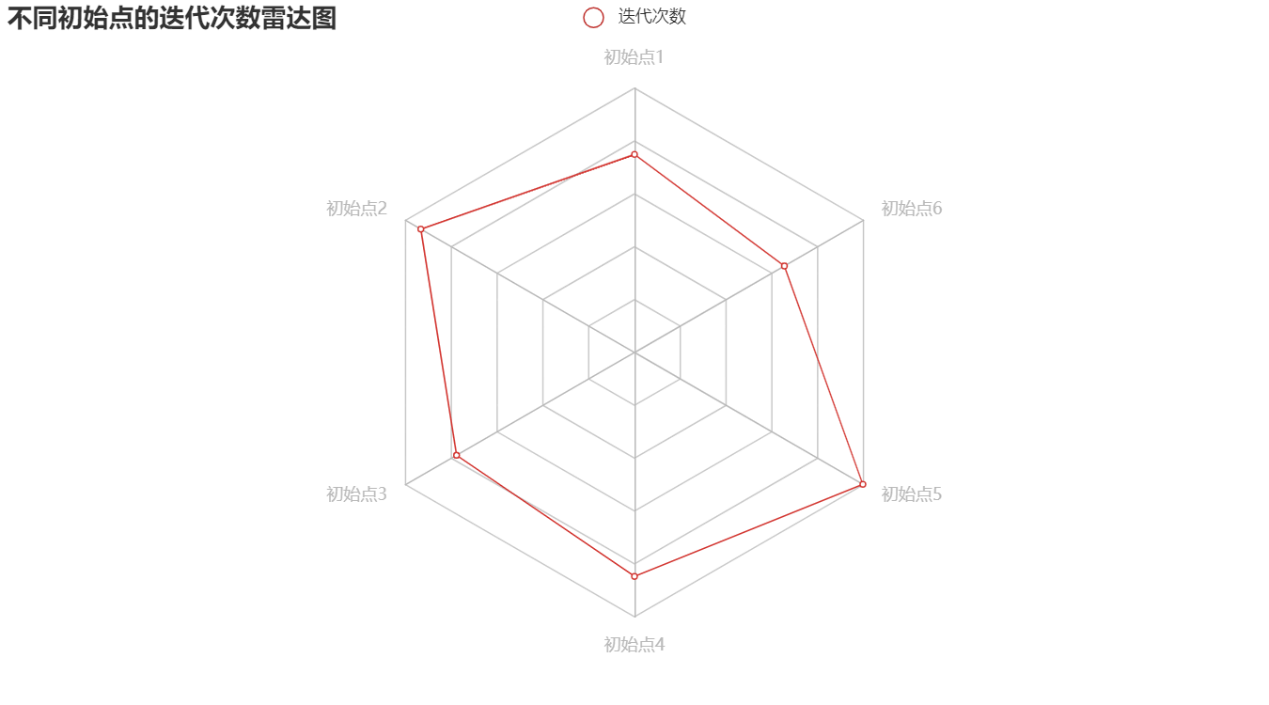
下图为，初始点与初始点的迭代次数对比雷达图
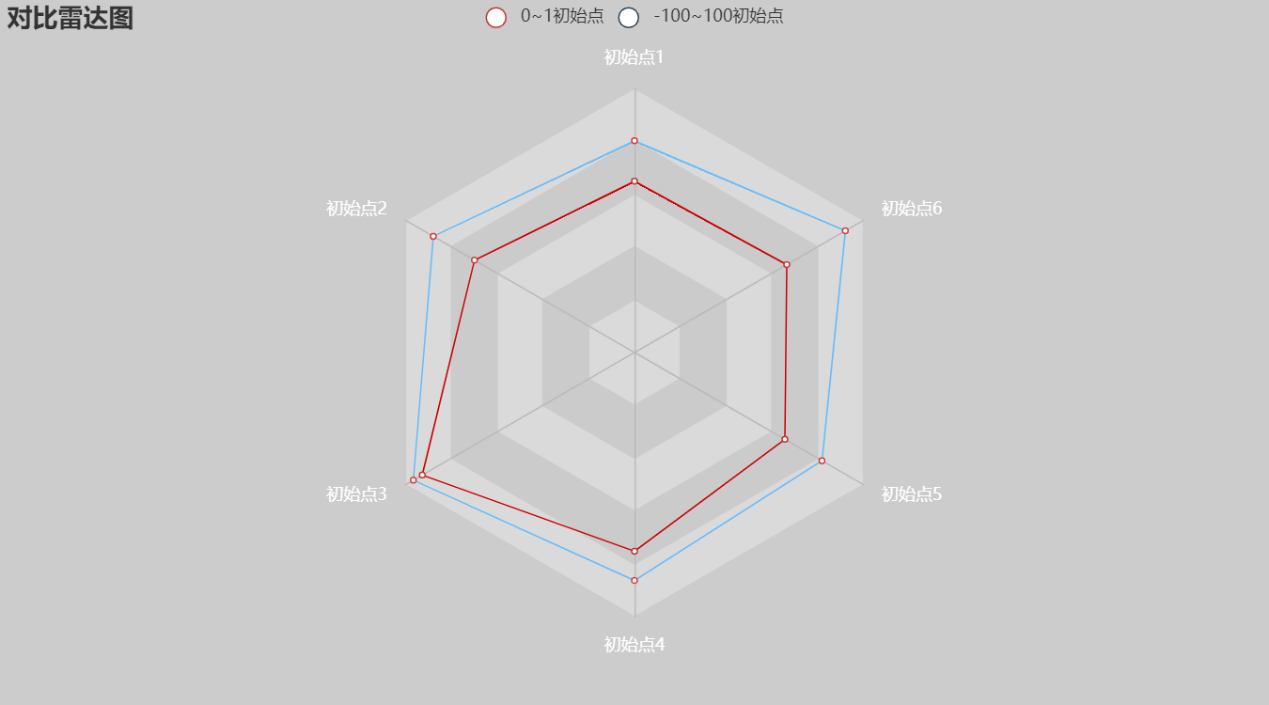
以上6次迭代最佳值：
初始点0,L-FBGS方法-armijo运行了0.7186863422393799s
初始点0,L-FBGS方法-armijo迭代了681次
初始点0,L-FBGS方法-armijo最优解的函数值为1.7947604723304925e-12
可以看出，红线即初始点被蓝线初始点包在里面，说明0-1初始点的迭代次数比初始点少，即更容易找到最优解。但从数据可以看出，两种初始点的迭代次数相差不大。从不同初始点出发，通过相差不大的迭代次数，都可以找到近似最优解，L-FBGS方法-armijo算法具有较好的稳定性。
参考资料：
《最优化：建模、算法与理论》,文再文、刘浩洋、户将
https://www.cnblogs.com/super-zhang-828/p/7991630.html
https://pyecharts.org/#/zh-cn/intro
更好阅读体验可以访问ModelWhale
工作台 - Heywhale.com
Copyright © 2012-2018 开丰娱乐-开丰注册登录绿色站 版权所有 琼ICP备xxxxxxxx号
电话：0898-08980898 手机：13876453617 地址：海南省海口市
在线咨询