0898-08980898 13876453617
是。先有分布函数,再有密度函数。密度函数是分布函数的导数。分布函数的重要性比密度函数大。
密度函数是和两个分布相关的。比如一般意义下的密度函数是一个分布相对于实数的勒贝格测度而言的。对于其他测度需要使用Radon-Nikodym微分。
简而言之,分布函数是直接和概率测度相关的。而密度函数需要另一个测度的参与,而且不一定存在。
不是。先有连续型变量的分布,然后在此基础上规定了连续,可微之类的条件,才能定义出概率密度函数。当概率密度函数存在,分布函数是一个定积分,变量X对于取值x的分布函数是X所在总体概率密度函数从负无穷到x的定积分,所以分布函数也叫累积分布函数。
不是。(不一定是。)
一个反例是服从Cantor分布的随机变量。该随机变量是连续的。CDF几乎处处连续,几乎处处可导,但是凡是可导的地方导数均为0。微积分基本定理不能成立,CDF虽然(几乎处处)连续可导但是没有密度。
事实上,任何singular continuous的随机变量均为反例。
但是,如果加上“密度存在”的大前提,原题答案则是肯定的:只要密度存在,密度一定为CDF的导数。
详见另外一题的小结
在连续随机变量中,概率密度函数(PDF)、概率分布函数、累积分布函数(CDF)之间的关系是什么? - 刘澈的回答欢迎斧正。
从数学上看,分布函数F(x)=P(X<x),表示随机变量X的值小于x的概率。这个意义很容易理解。概率密度f(x)是F(x)在x处的关于x的一阶导数,即变化率。如果在某一x附近取非常小的一个邻域Δx,那么,随机变量X落在(x, x+Δx)内的概率约为f(x)Δx,即P(x<X<x+Δx)≈f(x)Δx。换句话说,概率密度f(x)是X落在x处“单位宽度”内的概率。“密度”一词可以由此理解。
首先呢,我们不上来就搬出定义,解说定义,如果那样不就落入了俗套?和教科书一样难懂。此文的目的是让你彻底弄懂这2个函数是怎么来的,为什么会有这2个函数。
看图说话一下,
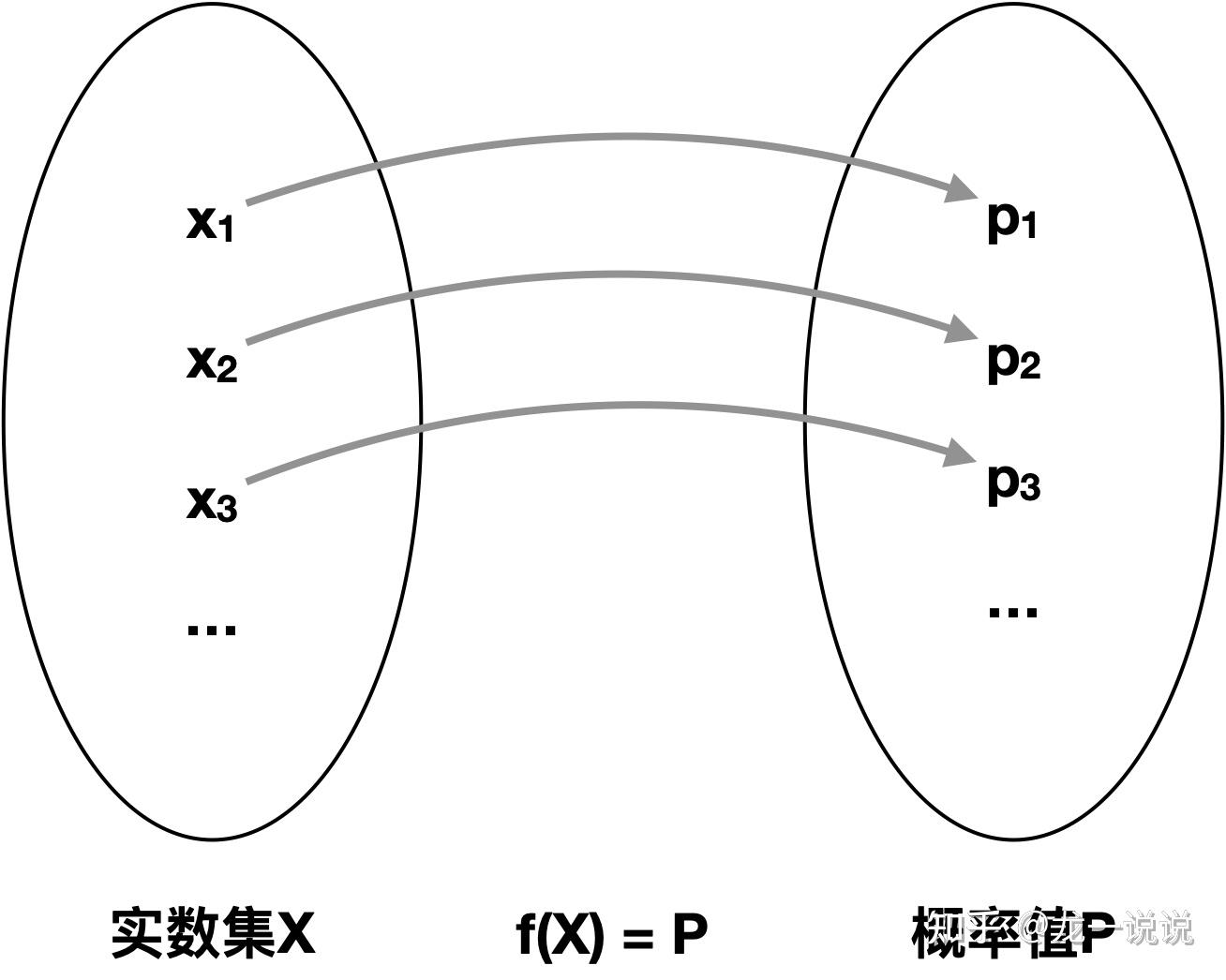
样本与样本点(就是自变量全体集合与自变量的单个取值)
随机试验E的所有基本结果组成的集合为E的样本空间。样本空间的元素称为样本点或基本事件,样本点小 表示样本集合大
的一个点
~ 所有样本点的集合
,或写作
~ 某一点的样本,也可以就用
表示
概率函数与单点概率值(因变量与单个因变量取值)
~ 所有样本对应的概率值集合,或者写作
,这里也可用
来表示,大家不要被迷惑了,这些都是同一种表达的不同符号表达方式而已
~ 某单样本对应的概率值,或者写作
其他写法:也可写成单个样本值 或
或
怎么做呢?某自变量是
找到一个函数 ,可以求解
,
这里都是同一个意思的不同写法而已,一开始上来就容易被教科书整晕
简而言之就是找到样本集合 对应的概率值
那么问题来了,如何找到这种映射函数?
任何事情都可以从最简单的开始,离散型看起来就比连续型好欺负
再用万能的掷骰子例子开始,其概率值为单点概率,且全部相等
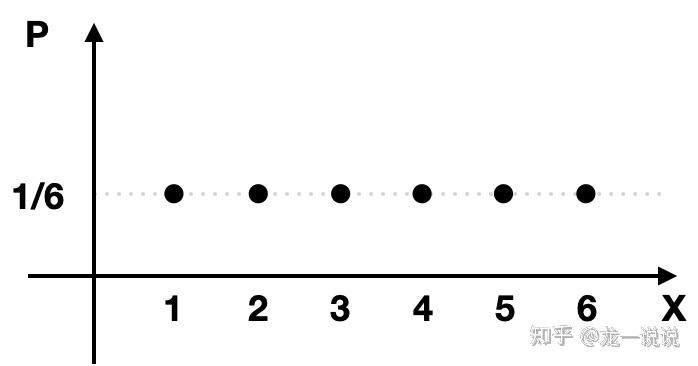
或者用分布律来表示
| X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
看起来很简单啊
留下一个问题,如果要表示范围概率怎么办?
简单!引入范围不就好了?根据概率的可列可加性(互斥)
既然把 叫做
,那么我们把
叫做
不就好了吗
大 的范围确实比小
的范围大啊...
所以在离散型数据可以这么用函数表示:
范围概率 ,其中
为某实数,
某单点概率值
离散型还是比较简单的。
好办啊,借助极限的思想,连续不就是离散趋于∞吗
先上图,还是掷骰子,这次这个骰子可以丢出1~6范围内的全体实数
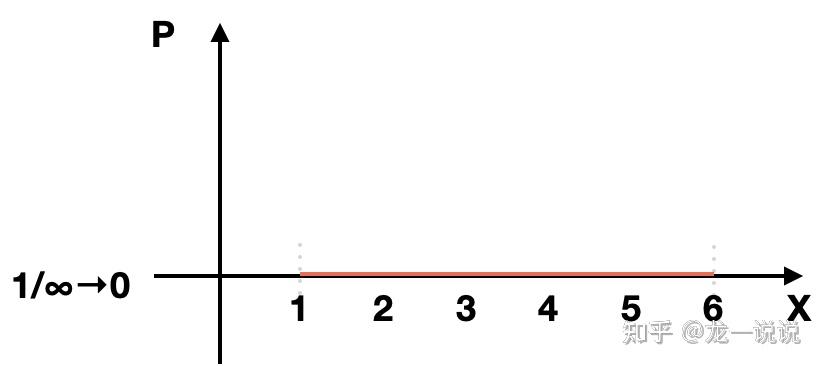
这一段实数是无穷多的,每一点的概率值趋近于0,怎么办???
单点概率值为0,上来就奔溃

我们需要一个新方法(苦思冥想中)
先把我们手上的牌摊出来

好像并没有什么X用啊
突然,想到有个大神,卡尔·皮尔逊(Karl Pearson)的直方图,能否有个类似这样的图?
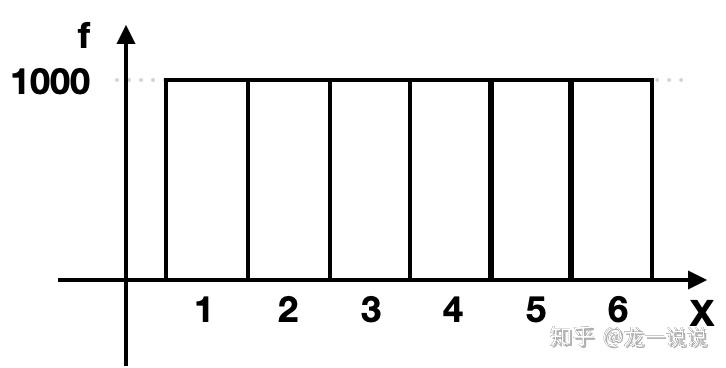
我们假设掷了6000次骰子,那么我们假设非常完美,每个数字出现1000次(实际当然会有出入,这里只是为了画图方便)
借助这个思路,我们构造一个函数
祭出我们的 ,且每个点发生的概率均等,那么
使得[a,b]发生概率均等,则新的函数
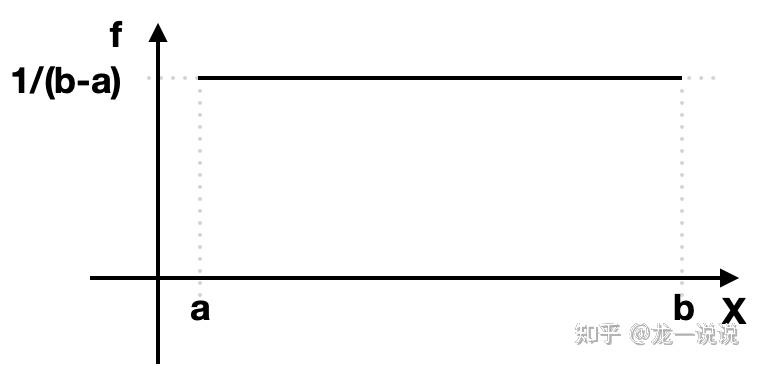
那么这个图怎么解释?这个函数叫什么名字?概率的概率?二阶概率?
每一点的函数值均为
想想分子分母分别代表什么意义, ,这里的
指的是范围概率
为距离,
为范围概率值,
就是每一段距离的概率均值
如果把每段距离取无穷小,这不就是导数的定义吗
回到正题,物理中, ,密度表示单位体积的质量,
那么我们把 称作概率密度,或者说单位距离的概率密度也就合理了
小声BB:其实不是叫 极小段的概率均值 不好么 哈哈,确实不够简洁
所以我们把新的 称作概率在ab段(距离d)的密度,概率密度
也就是说不引入概率密度这个表述,单点的概率值没有办法表示
任意概率密度函数
这里的 表示某一段距离的概率值
所以对于概率密度来说,
什么是无穷小:
无穷小是极限中的概念,就是无限趋近于0。
可以把无穷小之间的比较看成是某两个数趋近于0的速度比。
所以无穷小除以无穷小不一定等于无穷小,可以等于任何数
得看这两个无穷小的阶数
如何推导
从上文 继续推导,
两边同求积分,得到累计概率(或叫概率分布)函数
左边, 看作是无穷个
之和;右边求积分;
对于任意一段 的概率,借助积分的知识就可以用这个方式很容易的表示
,即ab
段
与
轴围成的面积大小
上文说的例子也可以成立:
表示某段实数对应的F 值,负无穷可以包含下限,因为下限到负无穷的概率可以为
,是等价的,只需要一个参数即可
F(X)就表示范围概率的函数,或者叫概率的分布函数
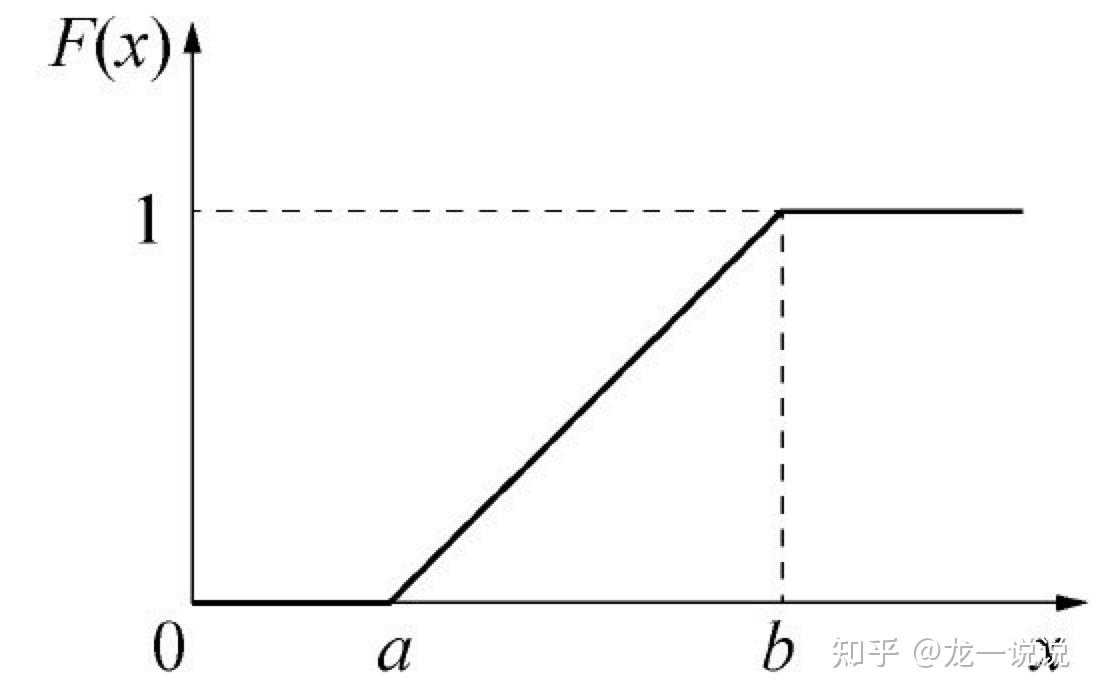
其实这也不一定是统计学家的思考过程,是我靠自己的知识推理的
概率密度函数,解决了单点概率值的表述可能性以及画图问题,还可以用面积(积分)来表示范围概率
概率分布函数,就是表述范围概率的函数值,单点概率的增速就是其导数,即概率密度
某单点概率值:
范围概率:
没有概率密度一说,单点非连续函数不可求导~
单点概率值:
单点概率密度值:
范围概率值:
码这么多字不容易,求个点赞 不过分吧